Reciprocal scaling with dcCA

Code 
# Paths
library(here)

# Multivariate analysis
library(ade4)
library(adegraphics)

# Matrix algebra
library(expm)

# Plots
library(CAnetwork)

Introduction

This is an extension of reciprocal scaling defined for correspondence analysis by Thioulouse and Chessel (1992) to double-constrained correspondence analysis.

Here, we have 3 matrices:

  • A data matrix \(Y\) (\(r \times c\))
  • A matrix of predictor variables \(E\) (\(r \times l\))
  • A matrix of predictor variables \(T\) (\(c \times k\))

(r <- dim(Y)[1])
[1] 26
(c <- dim(Y)[2])
[1] 21
(l <- ncol(E))
[1] 6
(k <- ncol(T_))
[1] 7
Code 
# Define bound for comparison to zero
zero <- 10e-10

Computation

From dcCA scores

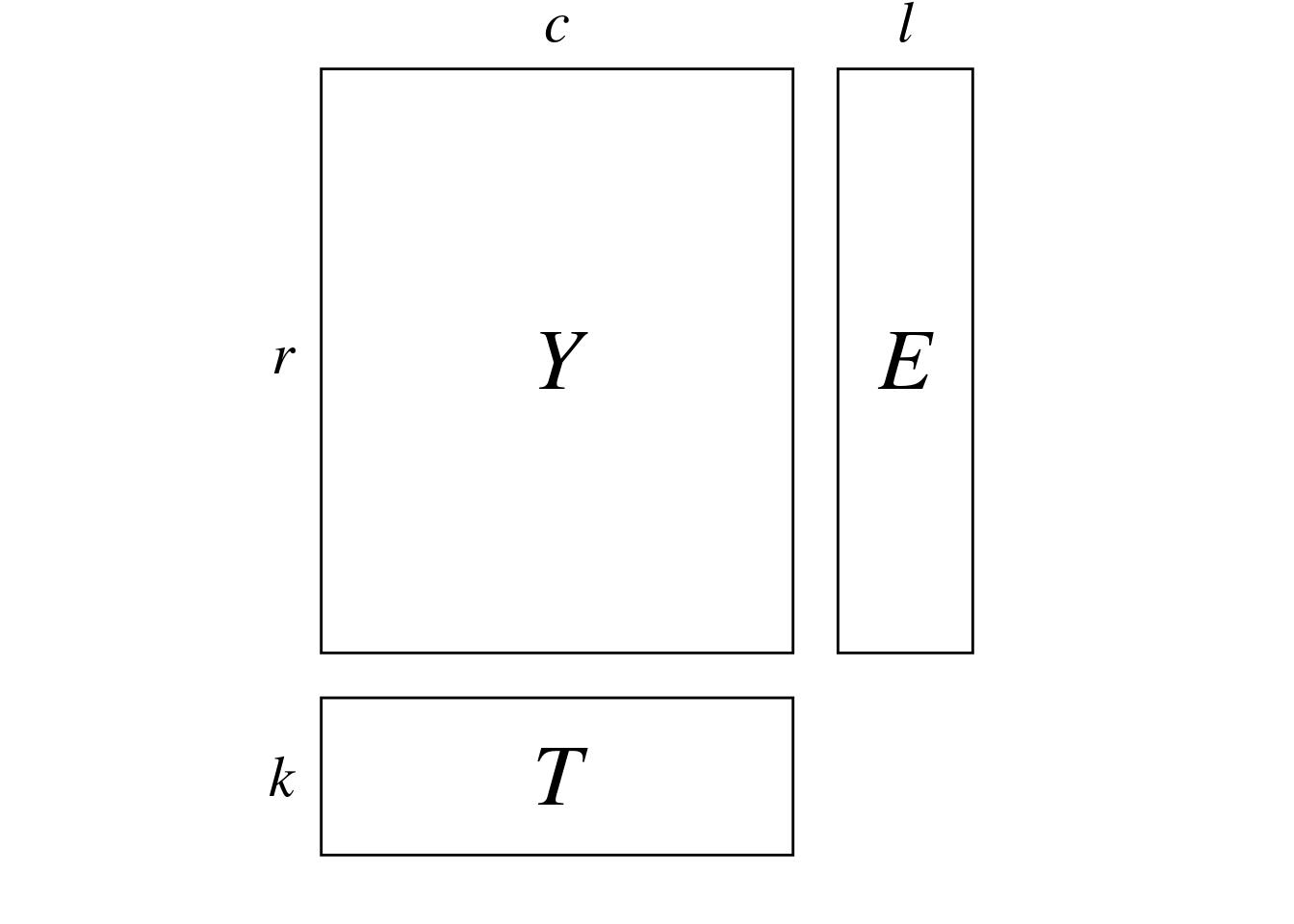
We compute the \(H_k(i, j)\) from the LC scores computed with dcCA (noted \(LC\) for rows LS scores and \(CC\) for columns LC scores). This formula is a direct extension of formula (11) in Thioulouse and Chessel (1992) but we replace the ordination scores obtained with CA with the ordination scores obtained with dcCA.

\[ H_k(i, j) = \frac{LC_k(i) + CC_k(j)}{\sqrt{2 \lambda_k \mu_k}} \]

Ydf <- as.data.frame(Y)
ca <- dudi.coa(Ydf, 
               scannf = FALSE,
               nf = min(r - 1, c - 1))

neig <- min(c(k, l))
dcca <- dpcaiv2(dudi = ca, 
                dfR = E,
                dfQ = T_,
                scannf = FALSE, 
                nf = neig)

L_dcca <- dcca$li
C_dcca <- dcca$co

lambda_dcca <- dcca$eig
mu_dcca <- 1 + sqrt(lambda_dcca)
# Transform matrix to count table
Yfreq <- as.data.frame(as.table(Y))
colnames(Yfreq) <- c("row", "col", "Freq")

# Remove the cells with no observation
Yfreq0 <- Yfreq[-which(Yfreq$Freq == 0),]
Yfreq0$colind <- match(Yfreq0$col, colnames(Y)) # match index and species names


# Initialize results matrix
H <- matrix(nrow = nrow(Yfreq0), 
            ncol = length(lambda_dcca))

for (kl in 1:length(lambda_dcca)) { # For each axis
  ind <- 1 # initialize row index
  for (obs in 1:nrow(Yfreq0)) { # For each observation
    i <- Yfreq0$row[obs]
    j <- Yfreq0$col[obs]
    H[ind, kl] <- (L_dcca[i, kl] + C_dcca[j, kl])/sqrt(2*lambda_dcca[kl]*mu_dcca[kl])
    ind <- ind + 1
  }
}

From canonical correlation analysis

To perform the canonical correlation analysis, we compute the inflated tables \(R\) (\(\omega \times l\)) and \(C\) (\(\omega \times k\)) from \(E\) (\(r \times l\)) and \(T\) (\(r \times k\)). \(R\) and \(C\) are respectively equivalents to \(E\) and \(T\) where rows of are duplicated as many times as there are correspondences in \(Y\).

We take the frequency table defined before and use it to compute the inflated tables (with weights):

# Create indicator tables
tabR <- acm.disjonctif(as.data.frame(Yfreq0$row))
tabR <- as.matrix(tabR) %*% as.matrix(E)
tabC <- acm.disjonctif(as.data.frame(Yfreq0$col))
tabC <- as.matrix(tabC) %*% as.matrix(T_)

# Get weights
wt <- Yfreq0$Freq

Below are the first lines of tables \(R\) and \(C\):

location elevation patch_area perc_forests perc_grasslands ShannonLandscapeDiv
0 10 6.28 7.7882 67.7785 0.232
0 30 7.92 16.4129 43.4066 0.274
0 430 83.24 24.4526 28.4995 0.274
0 420 140.83 41.9966 34.2412 0.260
0 400 140.83 41.9966 34.2412 0.260
0 500 0.50 7.5445 67.0780 0.240
0 470 7.84 19.3087 56.4031 0.253
0 110 21.15 23.4668 49.8908 0.262
0 460 24.82 21.3932 57.0430 0.243
0 450 3.11 4.8285 73.7518 0.216
0 40 6.66 7.4729 66.0061 0.240
0 160 5.63 32.3516 45.0477 0.253
0 160 10.99 29.7139 18.8270 0.291
1 10 6.28 7.7882 67.7785 0.232
1 30 7.92 16.4129 43.4066 0.274
1 430 83.24 24.4526 28.4995 0.274
1 420 140.83 41.9966 34.2412 0.260
1 400 140.83 41.9966 34.2412 0.260
1 500 0.50 7.5445 67.0780 0.240
1 470 7.84 19.3087 56.4031 0.253
1 110 21.15 23.4668 49.8908 0.262
1 460 24.82 21.3932 57.0430 0.243
1 450 3.11 4.8285 73.7518 0.216
1 40 6.66 7.4729 66.0061 0.240
1 160 5.63 32.3516 45.0477 0.253
1 160 10.99 29.7139 18.8270 0.291
0 160 10.99 29.7139 18.8270 0.291
1 500 0.50 7.5445 67.0780 0.240
1 460 24.82 21.3932 57.0430 0.243
1 450 3.11 4.8285 73.7518 0.216
biog forag mass diet move nest eggs
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 2 2 3 1 2 2
1 1 1 2 1 2 2
1 1 1 2 1 2 2
1 1 1 2 1 2 2
1 1 1 2 1 2 2

Then, we perform a canonical correlation on the scaled tables \(R_{scaled}\) and \(C_{scaled}\). We find the coefficients \(\rho\) and \(\gamma\) maximizing the correlation between the scores \(S_R = R_{scaled} \rho\) and \(S_C = C_{scaled} \gamma\).

# Center tables
tabR_scaled <- scalewt(tabR, wt, 
                       scale = FALSE)
tabC_scaled <- scalewt(tabC, wt, 
                       scale = FALSE)

res <- cancor(diag(sqrt(wt)) %*% tabR_scaled, 
              diag(sqrt(wt)) %*% tabC_scaled, 
              xcenter = FALSE, ycenter = FALSE)
# res gives the coefficients of the linear combinations that maximizes the correlation between the 2 dimensions
dim(res$xcoef) # l columns -> R_scaled is of full rank
[1] 6 6
dim(res$ycoef) # k columns -> C_scaled is of full rank
[1] 7 7
# Compute these scores from this coef
scoreR <- tabR_scaled[, 1:l]  %*% res$xcoef
scoreC <- tabC_scaled[, 1:k]  %*% res$ycoef

We have \(H = (S_R + S_C)_{scaled}\).

# Get H
scoreRC <- scoreR[, 1:l] + scoreC[, 1:l] # here we have l < k so l axes
scoreRC_scaled <- scalewt(scoreRC, wt = wt)
# Check result
all(abs(scoreRC_scaled/H) - 1 < 10e-10)
[1] TRUE

Plot

Code 
multiplot(indiv_row = H, 
          indiv_row_lab = paste0("site ", Yfreq0$row, "/", Yfreq0$col),
          row_color = "black", eig = lambda_dcca)

Conditional means and variances from RC scores

TL;DR

Once we have the correspondences scores, we can group them by row (site) or column (species) to compute conditional summary statistics:

  • conditional mean for site \(i\) or species \(j\) (for each axis \(k\))
  • conditional variance for site \(i\) or species \(j\) (for each axis \(k\))
  • conditional covariance for site \(i\) or species \(j\) (between axes \(k\) and \(l\))

These conditional statistics can be computed using \(H_k(i,j)\) (weighted means/variances/covariances) or using the dcCA scores. We only present the dcCA scores formulas below.

Formulas using dcCA scores

Rows (sites) Columns (species)
Mean for axis \(k\) \[m_k(i) = \frac{1}{\sqrt{2 \mu_k}} \times (LC1_k(i) + L_k(i))\] \[m_k(j) = \frac{1}{\sqrt{2 \mu_k}} \times (CC1_k(j) + C_k(j))\]
Variance for axis \(k\) \[s^2_k(i) = \frac{1}{2\lambda_k\mu_k} \left( \frac{1}{y_{i \cdot}} \sum_{j = 1}^c \left(y_{ij} CC_k^2(j) \right) - \lambda_k L_k^2(i) \right)\] \[s^2_k(j) = \frac{1}{2\lambda_k\mu_k} \left( \frac{1}{y_{\cdot j}} \sum_{i = 1}^r \left(y_{ij} LC_k^2(i) \right) - \lambda_k C_k^2(j) \right)\]
Covariance between axes \(k\), \(l\)

Let’s compare the means obtained from canonical correlations scores and the dcCA scores.

n <- sum(Y)

For rows = sites

Below is a graphical illustration of scoreRC grouped by rows:

s.class(scoreRC,
        wt = Yfreq0$Freq,
        fac = as.factor(Yfreq0$row),
        plabels.col = params$colsite, 
        main = "With RC score (points = correspondences)")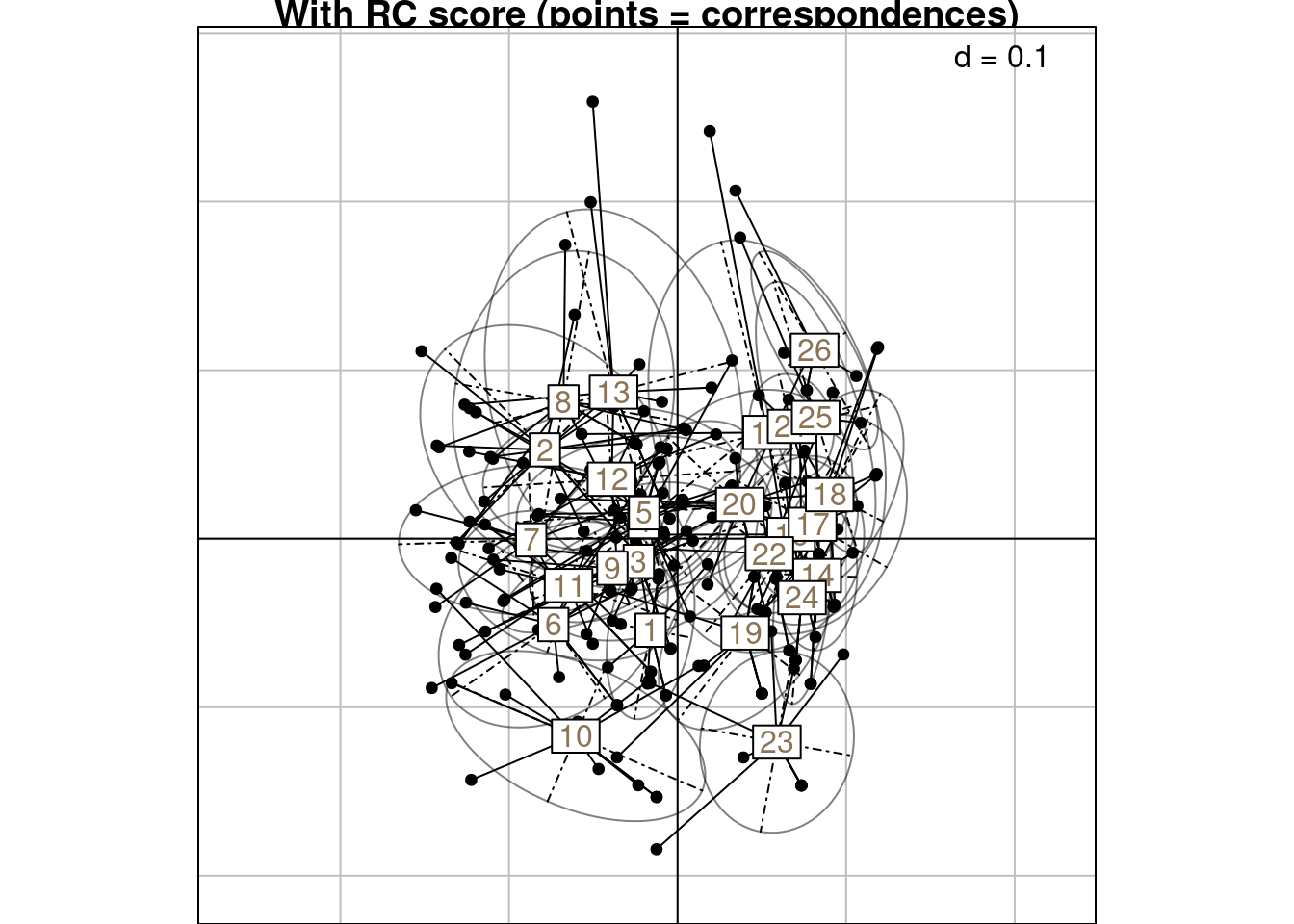

Formula with RC scores (definition)

mrowsRC <- meanfacwt(scoreRC_scaled, fac = Yfreq0$row, wt = Yfreq0$Freq)
mrowsRC/(as.matrix(dcca$l1 + dcca$lsR) %*% diag(1/sqrt(2*mu_dcca)))
   X1 X2 X3 X4 X5 X6
1  -1  1 -1  1 -1 -1
2  -1  1 -1  1 -1 -1
3  -1  1 -1  1 -1 -1
4  -1  1 -1  1 -1 -1
5  -1  1 -1  1 -1 -1
6  -1  1 -1  1 -1 -1
7  -1  1 -1  1 -1 -1
8  -1  1 -1  1 -1 -1
9  -1  1 -1  1 -1 -1
10 -1  1 -1  1 -1 -1
11 -1  1 -1  1 -1 -1
12 -1  1 -1  1 -1 -1
13 -1  1 -1  1 -1 -1
14 -1  1 -1  1 -1 -1
15 -1  1 -1  1 -1 -1
16 -1  1 -1  1 -1 -1
17 -1  1 -1  1 -1 -1
18 -1  1 -1  1 -1 -1
19 -1  1 -1  1 -1 -1
20 -1  1 -1  1 -1 -1
21 -1  1 -1  1 -1 -1
22 -1  1 -1  1 -1 -1
23 -1  1 -1  1 -1 -1
24 -1  1 -1  1 -1 -1
25 -1  1 -1  1 -1 -1
26 -1  1 -1  1 -1 -1
varrowsRC <- varfacwt(scoreRC_scaled, fac = Yfreq0$row, wt = Yfreq0$Freq)

Variance formula with dcCA scores

# Get marginal counts
yi_ <- rowSums(Y)
y_j <- colSums(Y)

varrows_dcca <- matrix(nrow = r, 
                       ncol = l)

for (i in 1:r) {
  # Get CCA scores for site i
  Li <- dcca$lsR[i, ]
  
  # Compute the part with the sum on Cj
  # we add all coordinates Cj^2 weighted by the number of observations on site i
  sumCj <- t(Y[i, ]) %*% as.matrix(dcca$co)^2

  # Fill i-th row with site i variance along each axis
  varrows_dcca[i, ] <- (1/(2*lambda_dcca*mu_dcca)) * (((1/yi_[i])*sumCj) - lambda_dcca*as.numeric(Li)^2)
}
varrowsRC/varrows_dcca
   X1 X2 X3 X4 X5 X6
1   1  1  1  1  1  1
2   1  1  1  1  1  1
3   1  1  1  1  1  1
4   1  1  1  1  1  1
5   1  1  1  1  1  1
6   1  1  1  1  1  1
7   1  1  1  1  1  1
8   1  1  1  1  1  1
9   1  1  1  1  1  1
10  1  1  1  1  1  1
11  1  1  1  1  1  1
12  1  1  1  1  1  1
13  1  1  1  1  1  1
14  1  1  1  1  1  1
15  1  1  1  1  1  1
16  1  1  1  1  1  1
17  1  1  1  1  1  1
18  1  1  1  1  1  1
19  1  1  1  1  1  1
20  1  1  1  1  1  1
21  1  1  1  1  1  1
22  1  1  1  1  1  1
23  1  1  1  1  1  1
24  1  1  1  1  1  1
25  1  1  1  1  1  1
26  1  1  1  1  1  1

For columns = species

Below is an illustration of the RC scores grouped by species.

s.class(scoreRC,
        wt = Yfreq0$Freq,
        fac = as.factor(Yfreq0$colind),
        lab = colnames(Y),
        plabels.col = params$colspp, 
        main = "With RC score (points = correspondences)")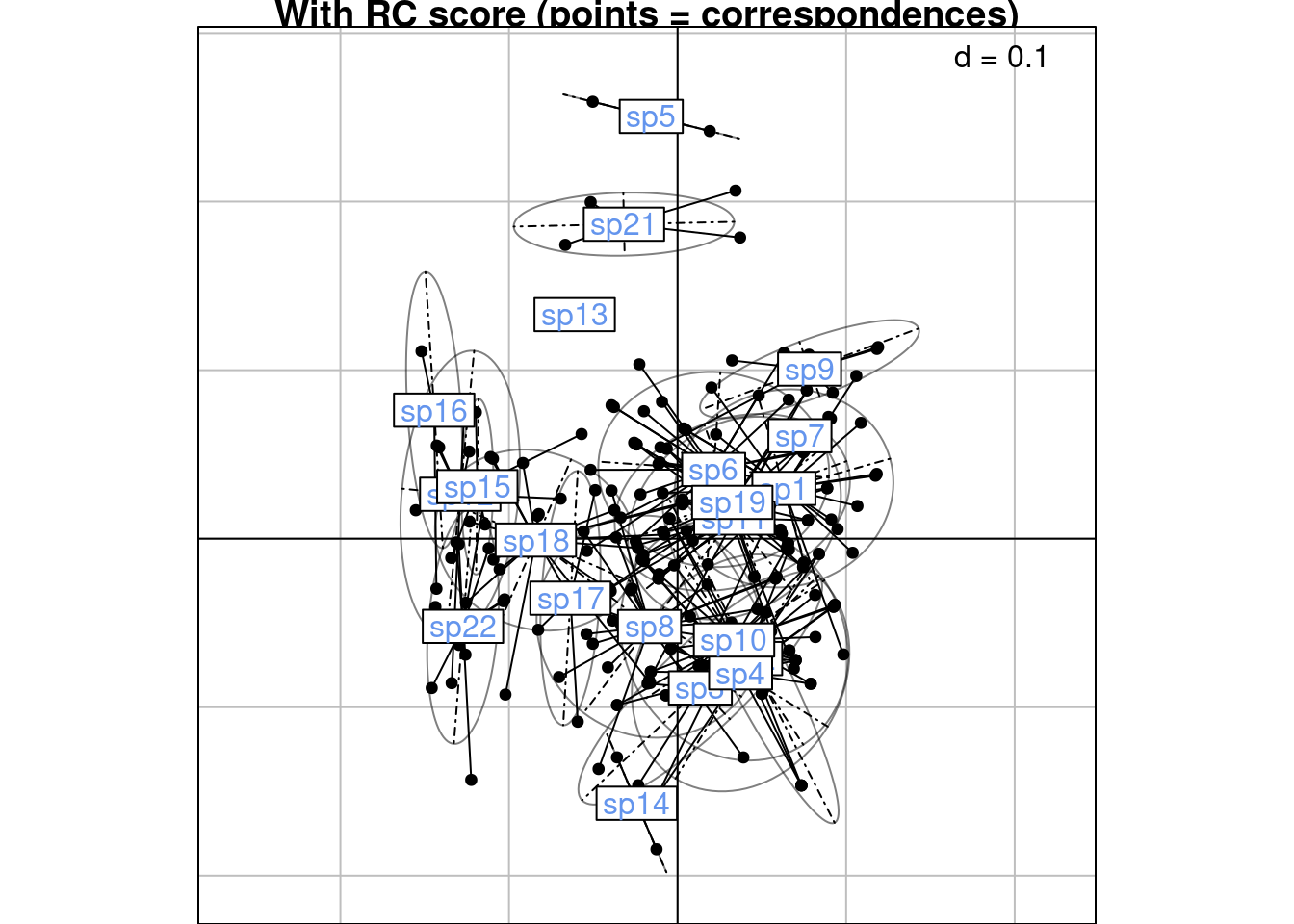

Formula with RC scores (definition)

mcolsRC <- meanfacwt(scoreRC_scaled, fac = Yfreq0$colind, wt = Yfreq0$Freq)

mcolsRC/(as.matrix(dcca$lsQ + dcca$c1) %*% diag(1/sqrt(2*mu_dcca)))
   X1 X2 X3 X4 X5 X6
1  -1  1 -1  1 -1 -1
2  -1  1 -1  1 -1 -1
3  -1  1 -1  1 -1 -1
4  -1  1 -1  1 -1 -1
5  -1  1 -1  1 -1 -1
6  -1  1 -1  1 -1 -1
7  -1  1 -1  1 -1 -1
8  -1  1 -1  1 -1 -1
9  -1  1 -1  1 -1 -1
10 -1  1 -1  1 -1 -1
11 -1  1 -1  1 -1 -1
12 -1  1 -1  1 -1 -1
13 -1  1 -1  1 -1 -1
14 -1  1 -1  1 -1 -1
15 -1  1 -1  1 -1 -1
16 -1  1 -1  1 -1 -1
17 -1  1 -1  1 -1 -1
18 -1  1 -1  1 -1 -1
19 -1  1 -1  1 -1 -1
20 -1  1 -1  1 -1 -1
21 -1  1 -1  1 -1 -1
varcolsRC <- varfacwt(scoreRC_scaled, fac = Yfreq0$colind, wt = Yfreq0$Freq)

Variance formula with dcCA scores

varcols_dcca <- matrix(nrow = c, 
                       ncol = l)

for (j in 1:c) {
  # Get CCA scores for species j
  Cj <- dcca$lsQ[j, ]
  
  # Compute the part with the sum on Li
  # we add all coordinates Li^2 weighted by the number of observations on species j
  sumLi <- t(Y[, j]) %*% as.matrix(dcca$li)^2

  # Fill i-th row with site i variance along each axis
  varcols_dcca[j, ] <- (1/(2*lambda_dcca*mu_dcca)) * (((1/y_j[j])*sumLi) - lambda_dcca*as.numeric(Cj)^2)
}
varcolsRC/varcols_dcca
   X1  X2 X3 X4 X5 X6
1   1   1  1  1  1  1
2   1   1  1  1  1  1
3   1   1  1  1  1  1
4   1   1  1  1  1  1
5   1   1  1  1  1  1
6   1   1  1  1  1  1
7   0   0  0  0  0  0
8   1   1  1  1  1  1
9   1   1  1  1  1  1
10  1   1  1  1  1  1
11  1   1  1  1  1  1
12  1   1  1  1  1  1
13  0 NaN  0  0  0  0
14  1   1  1  1  1  1
15  1   1  1  1  1  1
16  1   1  1  1  1  1
17  1   1  1  1  1  1
18  1   1  1  1  1  1
19  1   1  1  1  1  1
20  1   1  1  1  1  1
21  1   1  1  1  1  1

Conditional means and variances from R scores and C scores

TL;DR

For the scores computed with R scores and C scores, we have 3 types of formulas:

  • definition (weighted mean/variance/covariance)
  • formulas using the dcCA scores
  • relation with the RC scores

Here, we don’t show the definition.

Formulas using dcCA scores

  • using R score
Rows (sites) Columns (species)
Mean for axis \(k\) \[mR_k(i) = \frac{1}{\sqrt{n}} LC1_k(i)\] (\(LC1 =\) normed LC score ($l1)) \[mR_k(j) = \frac{1}{\sqrt{n}} C_k(j)\] (\(C =\) species WA score ($lsQ))
Variance for axis \(k\) None \[sR_k^2(j) = \frac{1}{n\lambda_k} \left( \frac{1}{y_{\cdot j}} \sum_{i = 1}^r \left(y_{ij} LC_k^2(i) \right) - \lambda_k C_k^2(j) \right)\]
Covariance between axes \(k\), \(l\)
  • using C score
Rows (sites) Columns (species)
Mean for axis \(k\) \[\frac{1}{\sqrt{n}} L_k(i)\] (\(L_k(i) =\) sites WA score ($lsR)) \[\frac{1}{\sqrt{n}} CC1_k(j)\] (\(CC1_k(j) =\) normed LC species score ($c1))
Variance for axis \(k\) \[sC_k^2(i) = \frac{1}{n\lambda_k} \left( \frac{1}{y_{i \cdot}} \sum_{j = 1}^c \left(y_{ij} CC_k^2(j) \right) - \lambda_k L_k^2(i) \right)\] None
Covariance between axes \(k\), \(l\)

Relation between RC scores and R score / C score

  • using R score
Rows (sites) Columns (species)
Mean for axis \(k\) \[mR_k(i) = \frac{\sqrt{2 \mu_k}}{\sqrt{n}} m_k(i) - \frac{1}{\sqrt{n}} L_k(i)\] \[mR_k(j) = \frac{\sqrt{2 \mu_k}}{\sqrt{n}} m_k(j) - \frac{1}{\sqrt{n}} CC1_k(j)\]
Variance for axis \(k\) None \(sR^2_k(j) = \frac{2\mu_k}{n} s^2_k(j)\)
Covariance between axes \(k\), \(l\)
  • using C score
Rows (sites) Columns (species)
Mean for axis \(k\) \[mC_k(i) = \frac{\sqrt{2 \mu_k}}{\sqrt{n}} m_k(i) - \frac{1}{\sqrt{n}} LC1_k(i)\] \[mC_k(j) = \frac{\sqrt{2 \mu_k}}{\sqrt{n}} m_k(j) - \frac{1}{\sqrt{n}} C_k(j)\]
Variance for axis \(k\) \(sC^2_k(i) = \frac{2\mu_k}{n} s^2_k(i)\) None
Covariance between axes \(k\), \(l\)

For rows = sites

scoreC

Below is a graphical illustration of scoreC grouped by rows:

s.class(scoreC,
        wt = Yfreq0$Freq,
        fac = as.factor(Yfreq0$row),
        ppoints.col = params$colspp,
        plabels.col = params$colsite, 
        main = "With C score (points = species scores)")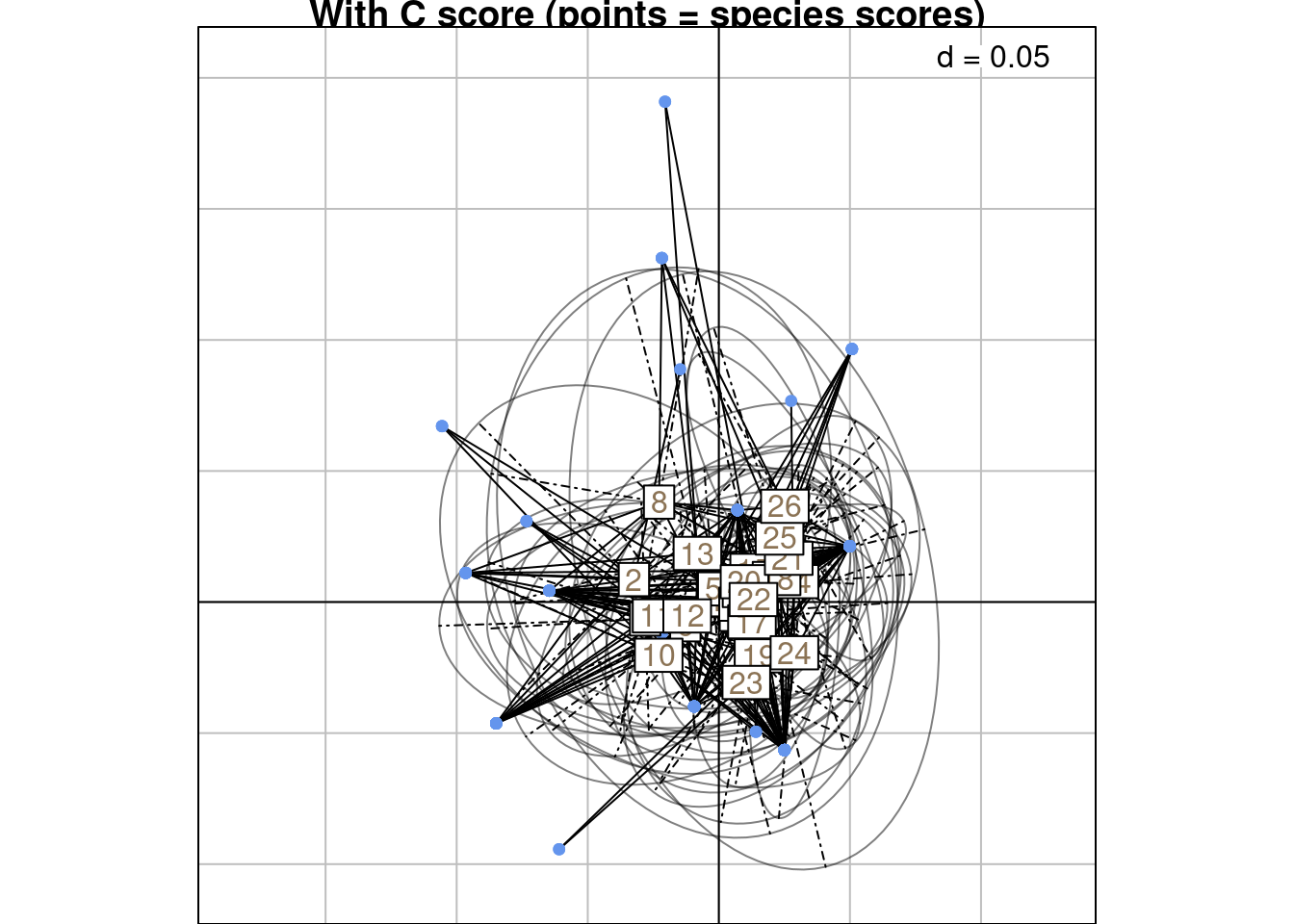

mrowsC <- meanfacwt(scoreC, fac = Yfreq0$row, wt = Yfreq0$Freq)

mrowsC/(dcca$lsR*1/sqrt(n))
   Axis1 Axis2 Axis3 Axis4 Axis5 Axis6
1     -1     1    -1     1    -1    -1
2     -1     1    -1     1    -1    -1
3     -1     1    -1     1    -1    -1
4     -1     1    -1     1    -1    -1
5     -1     1    -1     1    -1    -1
6     -1     1    -1     1    -1    -1
7     -1     1    -1     1    -1    -1
8     -1     1    -1     1    -1    -1
9     -1     1    -1     1    -1    -1
10    -1     1    -1     1    -1    -1
11    -1     1    -1     1    -1    -1
12    -1     1    -1     1    -1    -1
13    -1     1    -1     1    -1    -1
14    -1     1    -1     1    -1    -1
15    -1     1    -1     1    -1    -1
16    -1     1    -1     1    -1    -1
17    -1     1    -1     1    -1    -1
18    -1     1    -1     1    -1    -1
19    -1     1    -1     1    -1    -1
20    -1     1    -1     1    -1    -1
21    -1     1    -1     1    -1    -1
22    -1     1    -1     1    -1    -1
23    -1     1    -1     1    -1    -1
24    -1     1    -1     1    -1    -1
25    -1     1    -1     1    -1    -1
26    -1     1    -1     1    -1    -1

Now let’s compute the variance of scoreC per row:

varrowsC <- varfacwt(scoreC, fac = Yfreq0$row, wt = Yfreq0$Freq)

Compare it to the variance of the RC score:

varrowsC[, 1:ncol(varrowsRC)]/(varrowsRC %*% diag(2*mu_dcca/n))
   X1 X2 X3 X4 X5 X6
1   1  1  1  1  1  1
2   1  1  1  1  1  1
3   1  1  1  1  1  1
4   1  1  1  1  1  1
5   1  1  1  1  1  1
6   1  1  1  1  1  1
7   1  1  1  1  1  1
8   1  1  1  1  1  1
9   1  1  1  1  1  1
10  1  1  1  1  1  1
11  1  1  1  1  1  1
12  1  1  1  1  1  1
13  1  1  1  1  1  1
14  1  1  1  1  1  1
15  1  1  1  1  1  1
16  1  1  1  1  1  1
17  1  1  1  1  1  1
18  1  1  1  1  1  1
19  1  1  1  1  1  1
20  1  1  1  1  1  1
21  1  1  1  1  1  1
22  1  1  1  1  1  1
23  1  1  1  1  1  1
24  1  1  1  1  1  1
25  1  1  1  1  1  1
26  1  1  1  1  1  1
scoreR

Now, we compute the mean per row (site) from the row (sites) scores.

Below is a graphical illustration of scoreR grouped by rows:

s.class(scoreR,
        wt = Yfreq0$Freq,
        fac = as.factor(Yfreq0$row),
        ppoints.col = params$colsite,
        plabels.col = params$colsite, 
        main = "With R score (points = sites scores)")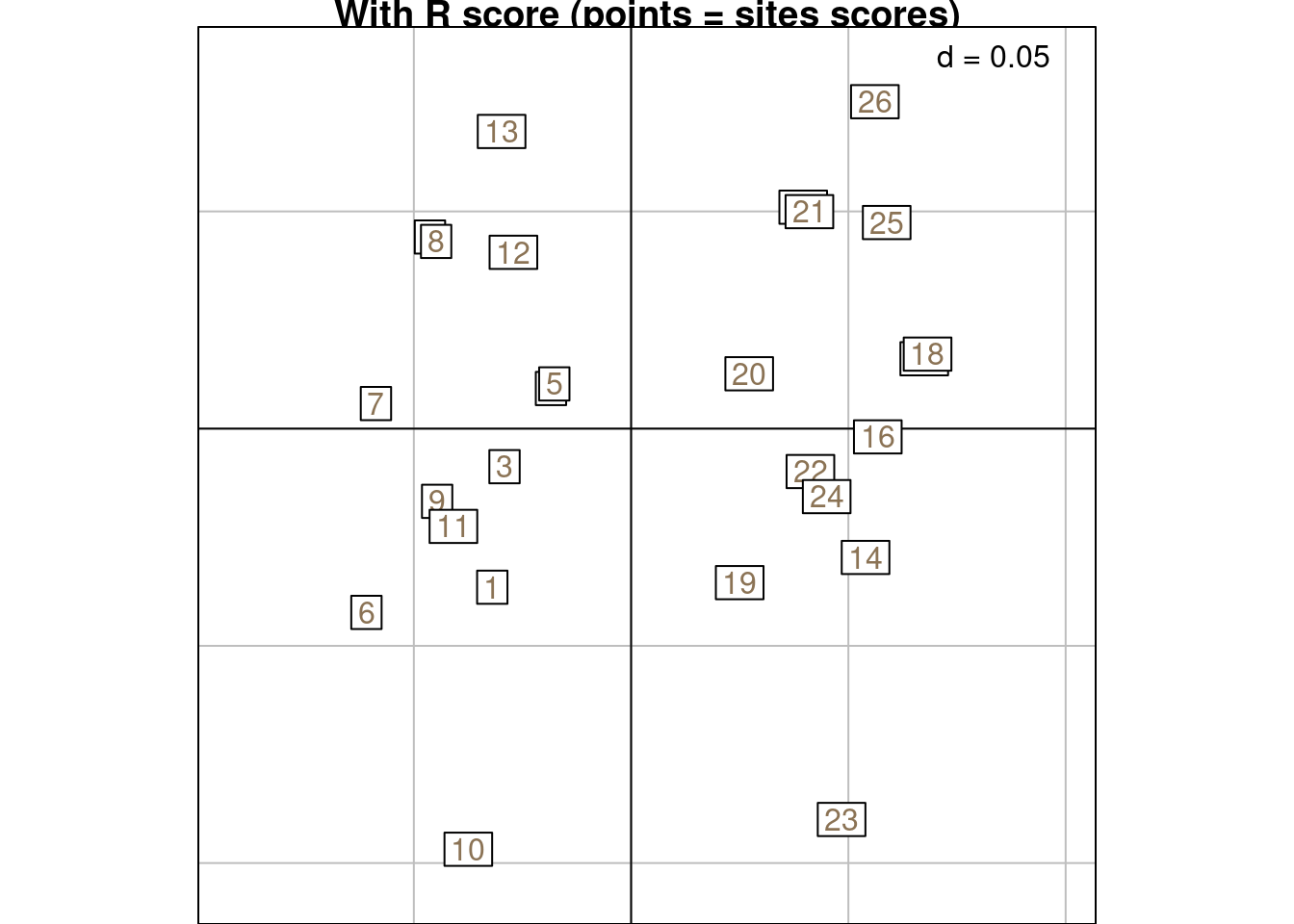

mrowsR <- meanfacwt(scoreR, fac = Yfreq0$row, wt = Yfreq0$Freq)

mrowsR/(dcca$l1*1/sqrt(n))
    RS1 RS2 RS3 RS4 RS5 RS6
X1   -1   1  -1   1  -1  -1
X2   -1   1  -1   1  -1  -1
X3   -1   1  -1   1  -1  -1
X4   -1   1  -1   1  -1  -1
X5   -1   1  -1   1  -1  -1
X6   -1   1  -1   1  -1  -1
X7   -1   1  -1   1  -1  -1
X8   -1   1  -1   1  -1  -1
X9   -1   1  -1   1  -1  -1
X10  -1   1  -1   1  -1  -1
X11  -1   1  -1   1  -1  -1
X12  -1   1  -1   1  -1  -1
X13  -1   1  -1   1  -1  -1
X14  -1   1  -1   1  -1  -1
X15  -1   1  -1   1  -1  -1
X16  -1   1  -1   1  -1  -1
X17  -1   1  -1   1  -1  -1
X18  -1   1  -1   1  -1  -1
X19  -1   1  -1   1  -1  -1
X20  -1   1  -1   1  -1  -1
X21  -1   1  -1   1  -1  -1
X22  -1   1  -1   1  -1  -1
X23  -1   1  -1   1  -1  -1
X24  -1   1  -1   1  -1  -1
X25  -1   1  -1   1  -1  -1
X26  -1   1  -1   1  -1  -1

The variance is null.

For columns = species

scoreC

We group the scoreC per species. Below is an illustration:

s.class(scoreC,
        wt = Yfreq0$Freq,
        fac = as.factor(Yfreq0$colind),
        lab = colnames(Y),
        ppoints.col = params$colspp,
        plabels.col = params$colspp, 
        main = "With C score (points = species scores)")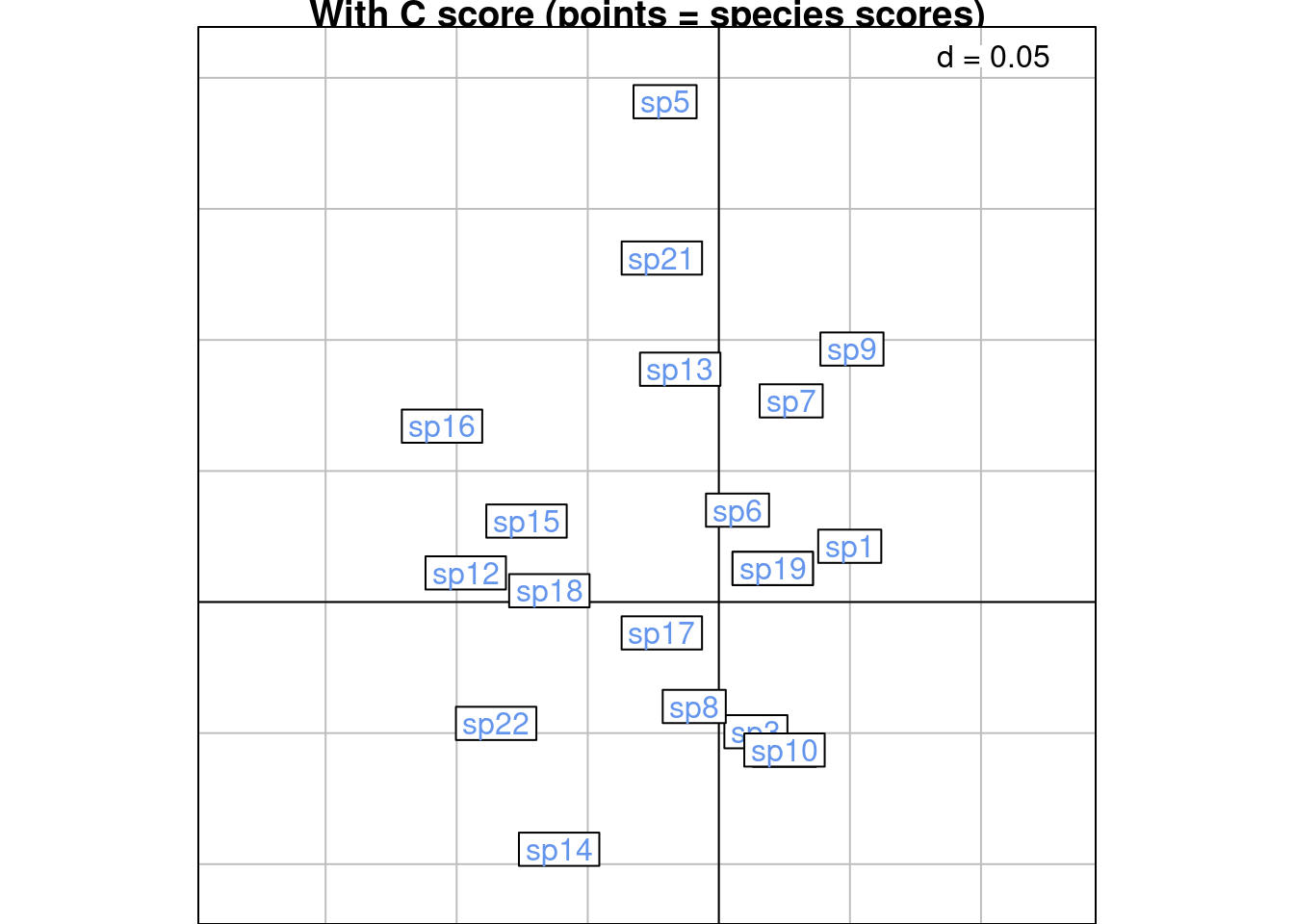

mcolsC <- meanfacwt(scoreC, fac = Yfreq0$colind, wt = Yfreq0$Freq)

mcolsC/(dcca$c1*1/sqrt(n))
     CS1 CS2 CS3 CS4 CS5 CS6
sp1   -1   1  -1   1  -1  -1
sp2   -1   1  -1   1  -1  -1
sp3   -1   1  -1   1  -1  -1
sp4   -1   1  -1   1  -1  -1
sp5   -1   1  -1   1  -1  -1
sp6   -1   1  -1   1  -1  -1
sp7   -1   1  -1   1  -1  -1
sp8   -1   1  -1   1  -1  -1
sp9   -1   1  -1   1  -1  -1
sp10  -1   1  -1   1  -1  -1
sp11  -1   1  -1   1  -1  -1
sp12  -1   1  -1   1  -1  -1
sp13  -1   1  -1   1  -1  -1
sp14  -1   1  -1   1  -1  -1
sp15  -1   1  -1   1  -1  -1
sp16  -1   1  -1   1  -1  -1
sp17  -1   1  -1   1  -1  -1
sp18  -1   1  -1   1  -1  -1
sp19  -1   1  -1   1  -1  -1
sp21  -1   1  -1   1  -1  -1
sp22  -1   1  -1   1  -1  -1

The variance is null.

scoreR

Below are the scoreR grouped by column:

s.class(scoreR,
        wt = Yfreq0$Freq,
        fac = as.factor(Yfreq0$colind),
        lab = colnames(Y),
        ppoints.col = params$colsite,
        plabels.col = params$colspp, 
        main = "With R score (points = sites scores)")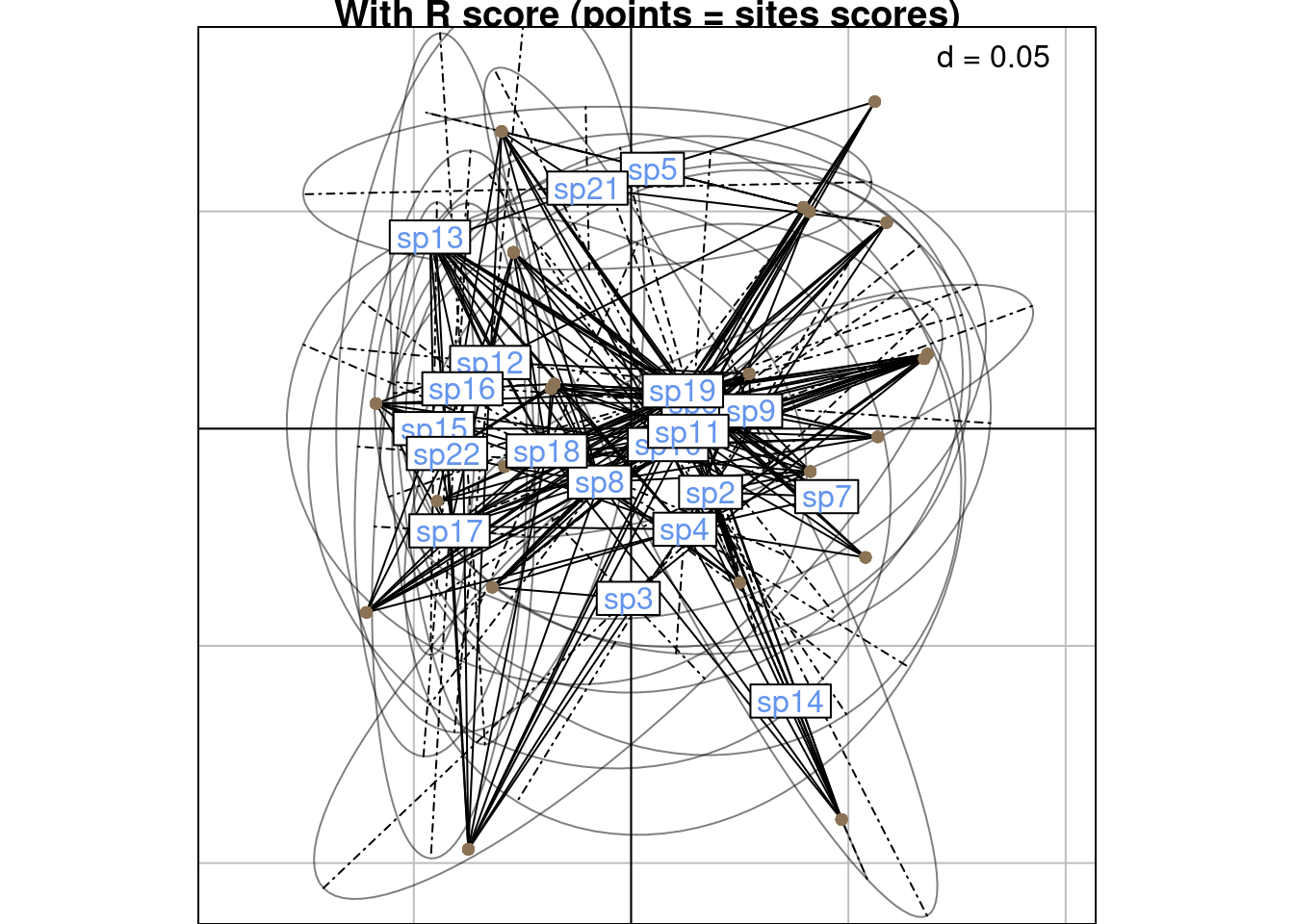

mcolsR <- meanfacwt(scoreR, fac = Yfreq0$colind, wt = Yfreq0$Freq)

mcolsR/(dcca$lsQ*1/sqrt(n))
     Comp1 Comp2 Comp3 Comp4 Comp5 Comp6
sp1     -1     1    -1     1    -1    -1
sp2     -1     1    -1     1    -1    -1
sp3     -1     1    -1     1    -1    -1
sp4     -1     1    -1     1    -1    -1
sp5     -1     1    -1     1    -1    -1
sp6     -1     1    -1     1    -1    -1
sp7     -1     1    -1     1    -1    -1
sp8     -1     1    -1     1    -1    -1
sp9     -1     1    -1     1    -1    -1
sp10    -1     1    -1     1    -1    -1
sp11    -1     1    -1     1    -1    -1
sp12    -1     1    -1     1    -1    -1
sp13    -1     1    -1     1    -1    -1
sp14    -1     1    -1     1    -1    -1
sp15    -1     1    -1     1    -1    -1
sp16    -1     1    -1     1    -1    -1
sp17    -1     1    -1     1    -1    -1
sp18    -1     1    -1     1    -1    -1
sp19    -1     1    -1     1    -1    -1
sp21    -1     1    -1     1    -1    -1
sp22    -1     1    -1     1    -1    -1

Now let’s compute the variance of scoreC per row:

varcolsR <- varfacwt(scoreR, fac = Yfreq0$colind, wt = Yfreq0$Freq)

Compare it to the variance of the RC score:

varcolsR/(varcolsRC %*% diag(2*mu_dcca/n))
    X1  X2  X3  X4  X5  X6
1    1   1   1   1   1   1
2    1   1   1   1   1   1
3    1   1   1   1   1   1
4    1   1   1   1   1   1
5    1   1   1   1   1   1
6    1   1   1   1   1   1
7  NaN NaN NaN NaN NaN NaN
8    1   1   1   1   1   1
9    1   1   1   1   1   1
10   1   1   1   1   1   1
11   1   1   1   1   1   1
12   1   1   1   1   1   1
13 NaN NaN NaN NaN NaN NaN
14   1   1   1   1   1   1
15   1   1   1   1   1   1
16   1   1   1   1   1   1
17   1   1   1   1   1   1
18   1   1   1   1   1   1
19   1   1   1   1   1   1
20   1   1   1   1   1   1
21   1   1   1   1   1   1

Means by RC scores as a mean of LC and WA scores

The means of the RC scores by row (site) \(m_k(i)\) multiplied by a scaling factor \(\sqrt{2\mu_k}\) are equal to $lsR+$l1.

Code 
# Invert first column
mrowsRC_inv <- mrowsRC
mrowsRC_inv[, 1] <- -mrowsRC_inv[, 1]
(mrowsRC_inv[, 1:2] %*% diag(sqrt(2*mu_dcca[1:2])))/(dcca$l1[, 1:2]+dcca$lsR[, 1:2])
    RS1 RS2
X1    1   1
X2    1   1
X3    1   1
X4    1   1
X5    1   1
X6    1   1
X7    1   1
X8    1   1
X9    1   1
X10   1   1
X11   1   1
X12   1   1
X13   1   1
X14   1   1
X15   1   1
X16   1   1
X17   1   1
X18   1   1
X19   1   1
X20   1   1
X21   1   1
X22   1   1
X23   1   1
X24   1   1
X25   1   1
X26   1   1

However, perhaps it is more intuitive to see the \(m_k(i)\) as the mean between $lsR and $l1: for that, we divide \(m_k(i) \times \sqrt{2\mu_k}\) by 2.

The graph below shows \(\frac{m_k(i) \times \sqrt{2\mu_k}}{2}\) along with the sites LS and WA scores. They are superimposed to the mean between $lsR and $l1 on the graph below:

Code 
# Create a long df with $lsR and $l1 for the plot
bindlsR <- dcca$lsR
colnames(bindlsR) <- colnames(dcca$l1)
lscores <- rbind(dcca$l1, bindlsR)
Code 
s.class(lscores,
        fac = as.factor(rep(rownames(Y), 2)),
        ppoints.col = params$colsite,
        wt = rep(dcca$lw, 2),
        plabels.col = params$colsite)
s.label((mrowsRC_inv %*% diag(sqrt(mu_dcca*2)/2)),
        plabels.col = "darkorchid3",
        add = TRUE)

Means of the not scaled scores

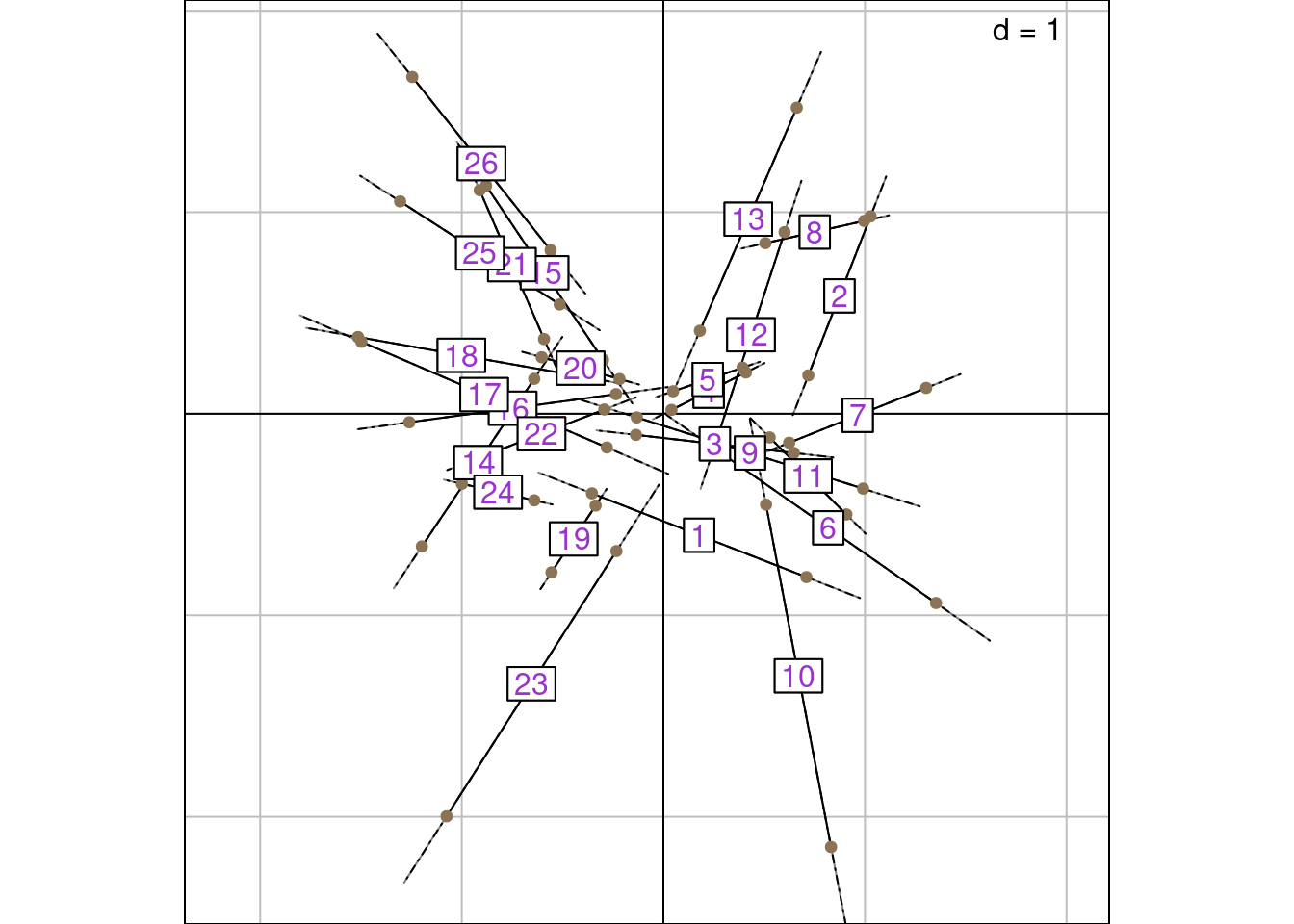
That was not too bad but it seems strange to compare LC1 and WA scores: LC and WA would be a better fit.

Code 
# Create a long df with $lsR and $l1 for the plot
bindlsR <- dcca$lsR
colnames(bindlsR) <- colnames(dcca$li)
lscores <- rbind(dcca$li, bindlsR)
Code 
s.class(lscores,
        fac = as.factor(rep(rownames(Y), 2)),
        ppoints.col = params$colsite,
        wt = rep(dcca$lw, 2),
        plabels.col = params$colsite)
s.label((mrowsRC_inv %*% diag(sqrt(mu_dcca*lambda_dcca*2)/2)),
        plabels.col = "darkorchid3",
        add = TRUE)

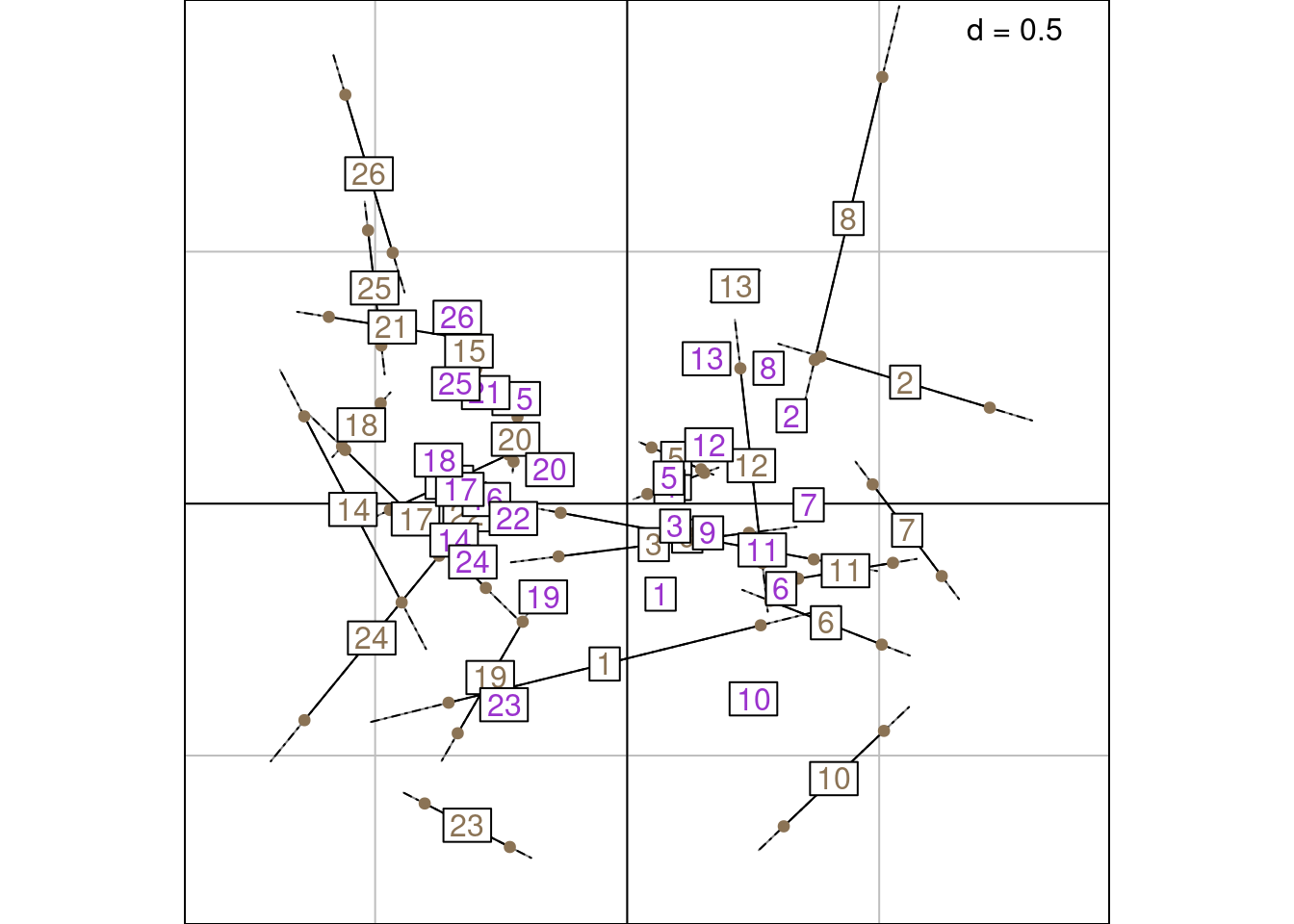
But then the mean of $lsR and $li is not superimposed to the means of the RC scores.

Non-reciprocal score

We can remain in the 2 biplots showing \(V\) with \(U^\star\) (c1 and lsR) (scaling type 1 = rows niches) and \(U\) and \(V^\star\) (lsQ and l1) (scaling type 2 = column niches).

\(H_1\) (scaling type 1, rows niches)

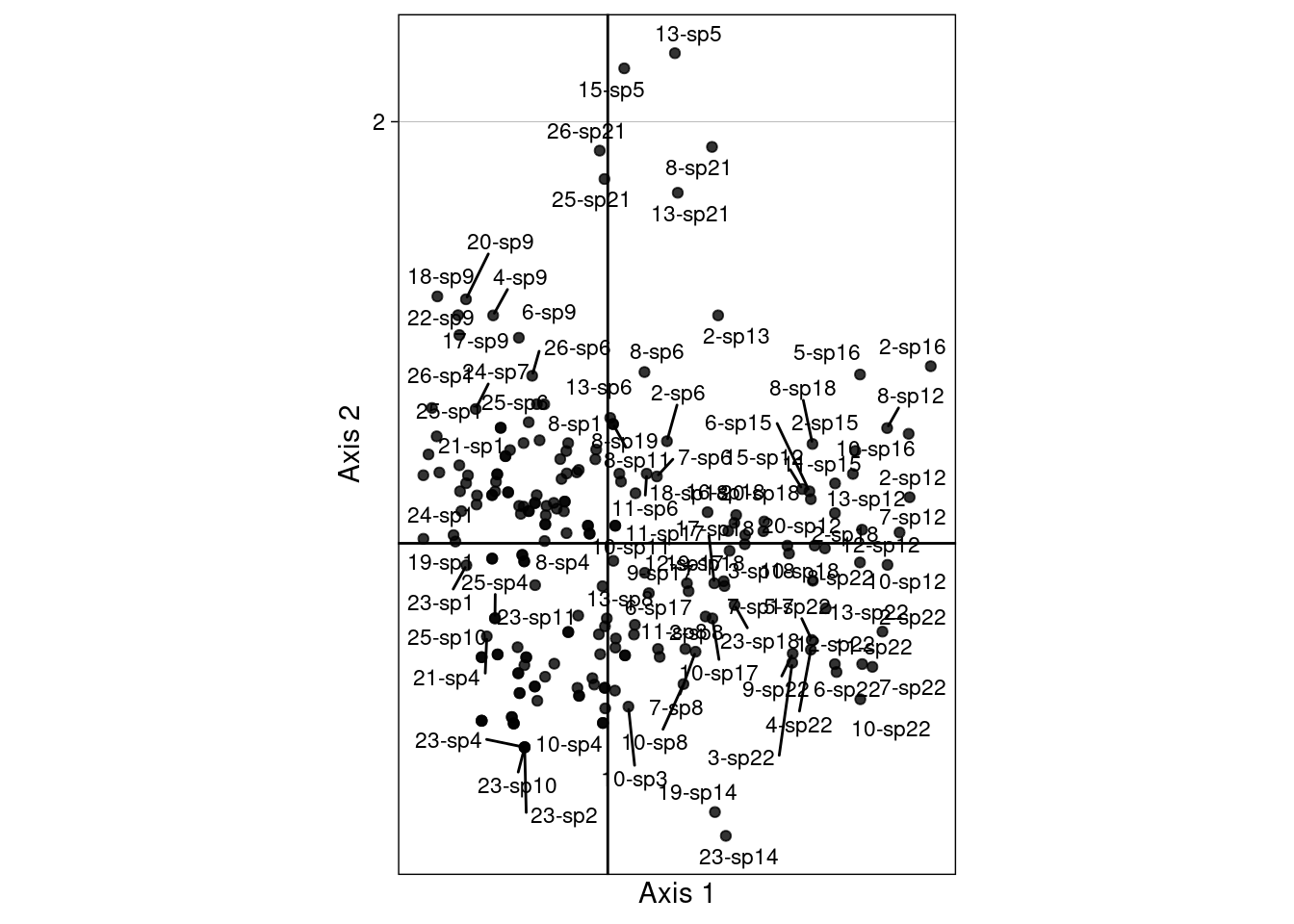
To do that, we define the “CA-correspondences” \(h1_k(i, j)\) for scaling type 1:

\[h1_k(i, j) = \frac{u^\star_k(i) + v_k(j)}{2}\]

Code 
# Initialize results matrix
H1 <- matrix(nrow = nrow(Yfreq0), 
             ncol = length(lambda_dcca))

for (k in 1:length(lambda_dcca)) { # For each axis
  ind <- 1 # initialize row index
  for (obs in 1:nrow(Yfreq0)) { # For each observation
    i <- Yfreq0$row[obs]
    j <- Yfreq0$col[obs]
    H1[ind, k] <- (dcca$lsR[i, k] + dcca$c1[j, k])/2
    ind <- ind + 1
  }
}
Code 
corresp <- paste(Yfreq0$row, Yfreq0$col, sep = "-")
multiplot(indiv_row = as.data.frame(H1), 
          indiv_row_lab = corresp,
          row_color = "black")

# Groupwise mean
mrows_nr <- meanfacwt(H1, fac = Yfreq0$row, wt = Yfreq0$Freq)
all(abs(abs(mrows_nr/dcca$lsR) - 1) < zero)
[1] TRUE
head(mrows_nr/mrowsRC) # It is different from the reciprocal scaling means
          X1        X2         X3          X4         X5          X6
1  1.6533866 0.5279337  0.5851892 -0.06781125 -0.1427069 -0.52991699
2 -0.6823573 0.2621430 -0.5942531  0.45270450 -0.5003293 -0.35482135
3  0.4415413 0.5643021 -0.5909733 -0.06788904  0.2459682  0.16148020
4 -0.1482127 0.1372513 -0.3383964  0.46228036  0.0820352 -0.32748383
5 -0.1818639 0.5279171 -0.2356614  0.11017165 -0.1671877  1.47696811
6 -0.2874715 0.2745043 -0.0337867  0.91463113  0.2885318 -0.05672653
# Groupwise variance
varrows_nr <- varfacwt(H1, fac = Yfreq0$row, wt = Yfreq0$Freq)
res <- varrows_nr %*% diag(2/mu_dcca) # factor 2/mu
all(abs(res/varrowsRC - 1) < zero)
[1] TRUE
# We could also multiply H1 before computing the variance
H1_scaled <- H1 %*% diag(sqrt(2/mu_dcca)) # Factor sqrt(2/mu)
varrows_nr_scaled <- varfacwt(H1_scaled, fac = Yfreq0$row, wt = Yfreq0$Freq)
all(abs(varrows_nr_scaled/varrowsRC - 1) < zero)
[1] TRUE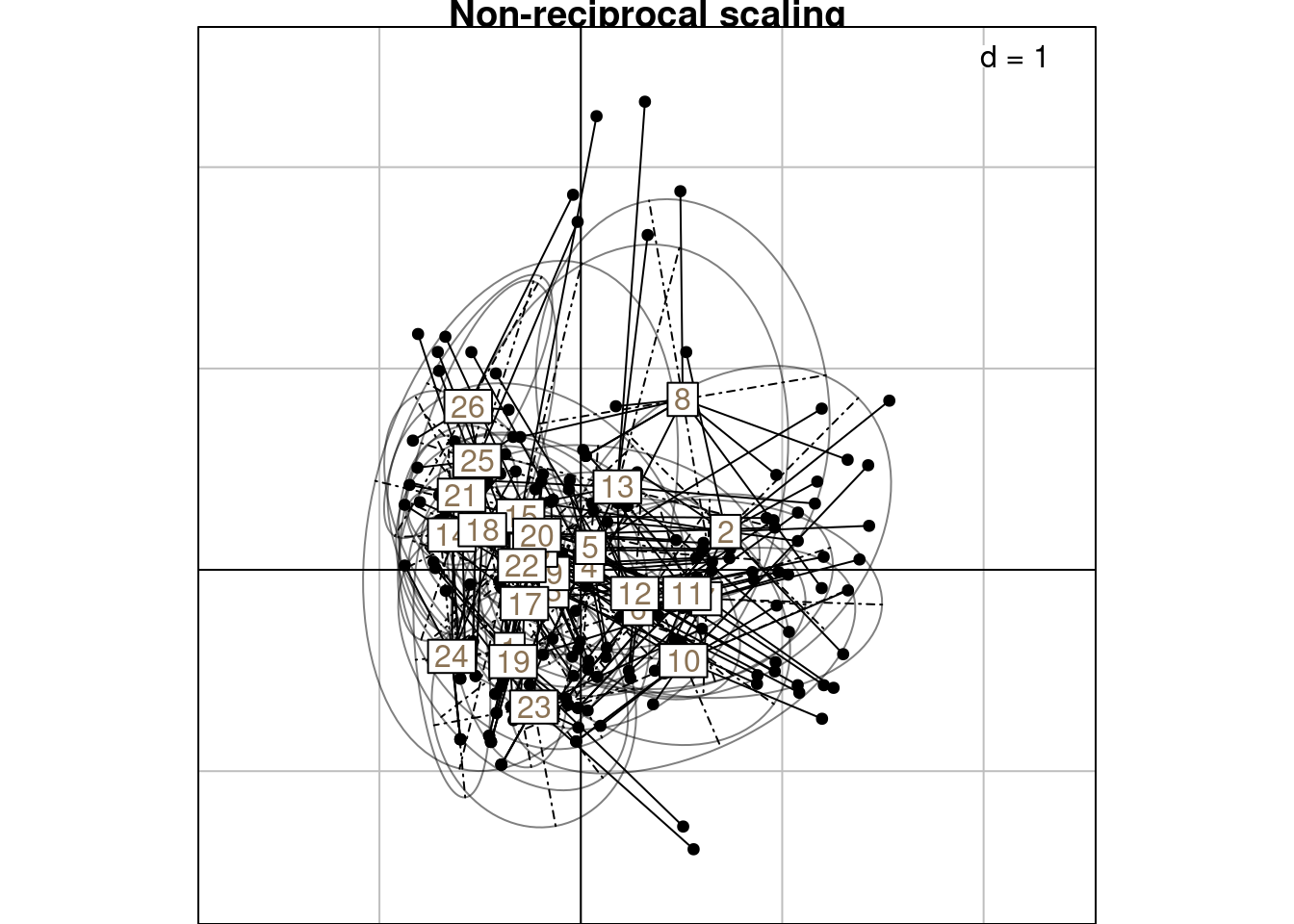
Code 
s.class(H1, 
        fac = Yfreq0$row, plabels.col = params$colsite, 
        wt = Yfreq0$Freq,
        main = "Non-reciprocal scaling")

Code 
s.class(H,
        fac = Yfreq0$row, plabels.col = params$colsite, 
        wt = Yfreq0$Freq,
        main = "Reciprocal scaling")

\(h1_k(i, j)\) can also be defined from the canonical correlation scores:

\[h1_k(i, j) = \frac{\sqrt{n} (R \bar{S_C} + S_C)}{2}\] where \(R \bar{S_C}\) corresponds to the duplicated version of \(\bar{S_C}\), the mean of C-scores by rows.

res <- meanfacwt(scoreC, fac = Yfreq0$row, wt = Yfreq0$Freq) # get the mean of scoreC by row
tabR <- as.matrix(acm.disjonctif(as.data.frame(Yfreq0$row)))
scoreRls <- tabR %*% res # Duplicate means according to correspondences of R

# Find back the formula from the scores 
H1_cancor <- (sqrt(n)*(scoreRls[, 1:l] + scoreC[, 1:l]))/2
# H1_cancor_scaled <- scalewt(H1_cancor, wt = wt/sum(wt))

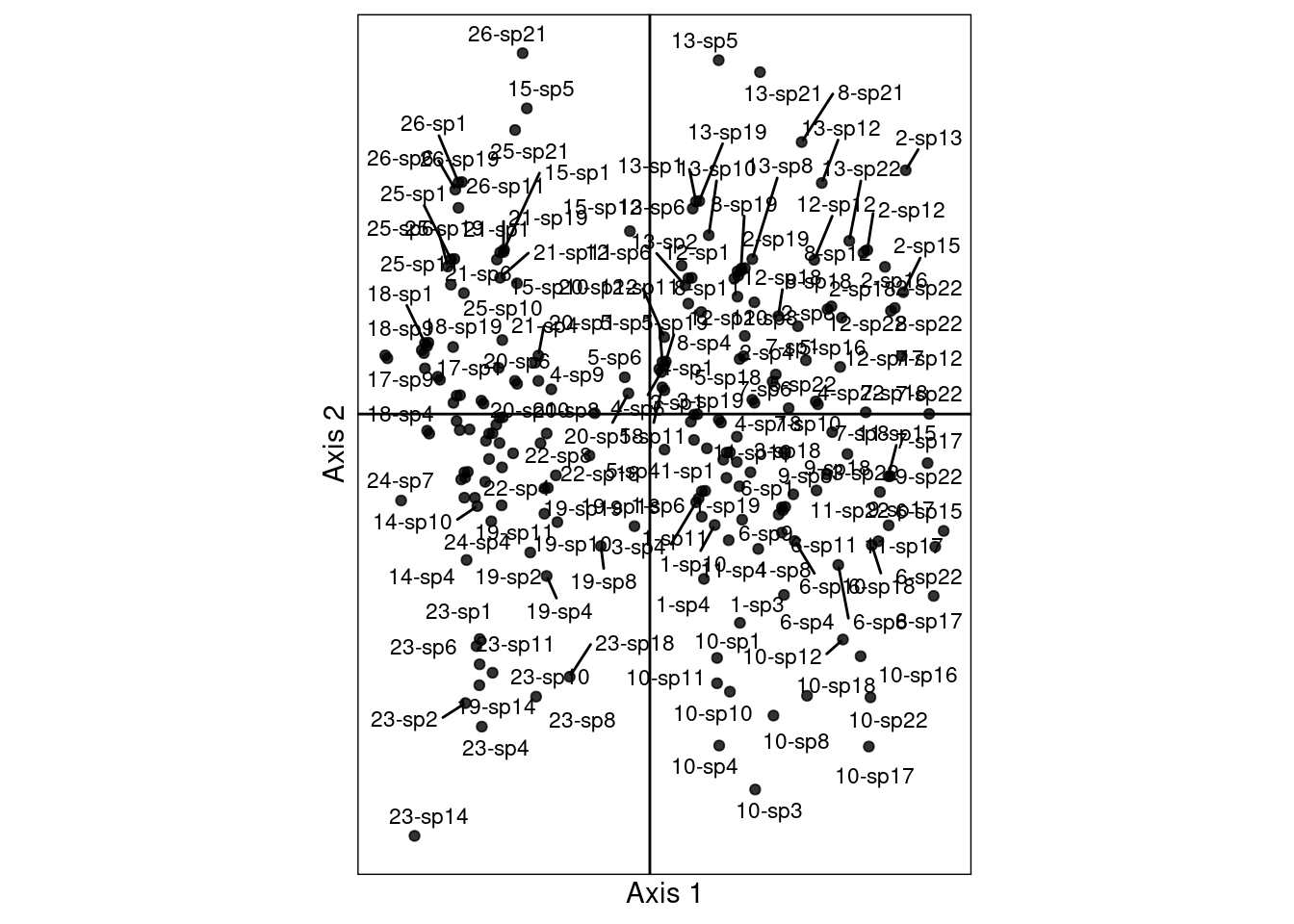
all(abs(abs(H1_cancor/H1) - 1) < zero)
[1] TRUE

\(H_2\) (scaling type 2, columns niches)

We define the “CA-correspondences” \(h2_k(i, j)\) for scaling type 2:

\[h2_k(i, j) = \frac{u_k(i) + v^\star_k(j)}{2}\]

Code 
# Initialize results matrix
H2 <- matrix(nrow = nrow(Yfreq0), 
             ncol = length(lambda_dcca))

for (k in 1:length(lambda_dcca)) { # For each axis
  ind <- 1 # initialize row index
  for (obs in 1:nrow(Yfreq0)) { # For each observation
    i <- Yfreq0$row[obs]
    j <- Yfreq0$col[obs]
    H2[ind, k] <- (dcca$l1[i, k] + dcca$lsQ[j, k])/2
    ind <- ind + 1
  }
}
Code 
corresp <- paste(Yfreq0$row, Yfreq0$col, sep = "-")
multiplot(indiv_row = as.data.frame(H2), 
          indiv_row_lab = corresp,
          row_color = "black")

# Groupwise mean
mcols_nr <- meanfacwt(H2, fac = Yfreq0$col, wt = Yfreq0$Freq)
all(abs(abs(mcols_nr/dcca$lsQ)-1) < zero)
[1] TRUE
head(mcols_nr/mcolsRC) # It is different from the reciprocal scaling means
             X1        X2         X3          X4          X5          X6
sp1 -0.34539825 0.4613888 -0.1291876  0.59460911  0.05862701 -0.06963278
sp2 -0.69971219 0.3321361 -0.7654332 18.27788124 -0.85018616 -1.39038985
sp3  0.08000112 0.7109524 -0.3302009  0.40289677 -1.17113661 -0.25880816
sp4 -0.54804851 0.4688067 -0.2190234  0.75729851  0.70129907 -1.27143300
sp5  0.52038835 0.3837661 -0.3593968 -0.03308342 -0.76039465 -2.17864998
sp6 -1.10639827 0.2343722 -5.0626170 -0.15807737 -0.18222986  0.02268947
# Groupwise variance
sp1 <- c(7, 13) # Species only present in one site
varcols_nr <- varfacwt(H2, fac = Yfreq0$col, wt = Yfreq0$Freq)
res <- varcols_nr %*% diag(2/mu_dcca)
all(abs(res[-sp1, ]/varcolsRC[-sp1, ] - 1) < zero) # Factor 2/mu
[1] TRUE
Code 
fac_col <- Yfreq0$col
s.class(H2, 
        fac = fac_col, plabels.col = params$colspp, 
        wt = Yfreq0$Freq,
        main = "Non-reciprocal scaling")

Code 
s.class(H, 
        fac = fac_col, plabels.col = params$colspp, 
        wt = Yfreq0$Freq,
        main = "Reciprocal scaling")

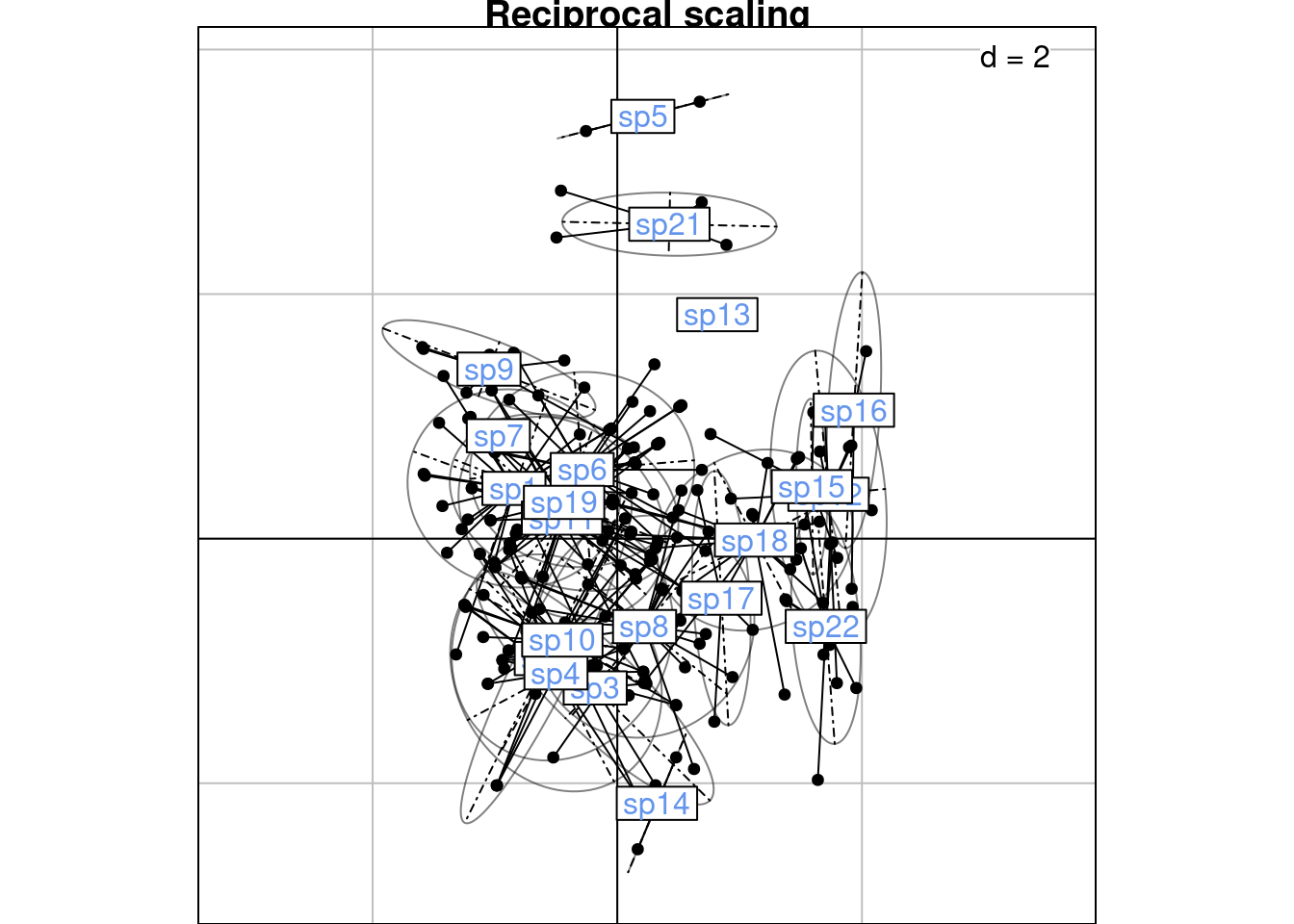
\(h2_k(i, j)\) can also be defined from the canonical correlation scores:

\[h2_k(i, j) = \frac{\sqrt{n} (S_R + C \bar{S_R})}{2}\]

where \(C \bar{S_R}\) corresponds to the duplicated version of \(\bar{S_R}\), the mean of R-scores by columns.

# ScoreR = l1
# ScoreC = c1
# mean of score C = ls

res <- meanfacwt(scoreR, fac = Yfreq0$col, wt = Yfreq0$Freq) # get the mean of scoreR by col
tabC <- as.matrix(acm.disjonctif(as.data.frame(Yfreq0$col)))
scoreCls <- tabC %*% res # Duplicate means according to correspondences of R

# Find back the formula from the scores 
H2_cancor <- (sqrt(n)*(scoreR[, 1:l] + scoreCls[, 1:l]))/2

all(abs(abs(H2_cancor/H2) - 1) < zero)
[1] TRUE

References

Thioulouse, Jean, and Daniel Chessel. 1992. “A Method for Reciprocal Scaling of Species Tolerance and Sample Diversity: Ecological Archives.” Ecology 73 (2): 670–80. https://doi.org/10.2307/1940773.