Code
# Paths
library(here)
# Multivariate analysis
library(ade4)
library(adegraphics)
# Matrix algebra
library(expm)
# Plots
library(CAnetwork)
library(patchwork)
library(ggplot2)Double constrained Correspondence Analysis (dc-CA)
Code
# Define bound for comparison to zero
zero <- 10e-10Code
#' Normalize row or columns vectors of a matrix
#'
#' @param M the matrix to normalize
#' @param margin the margin (1 = rows, 2 = columns)
#'
#' @return The normalized matrix M
normalize <- function(M, margin) {
m_norm <- apply(M,
margin,
function(x) sqrt(sum(x^2)))
M_norm <- sweep(M, margin, m_norm, "/")
return(M_norm)
}The contents of this page relies heavily on Braak, Šmilauer, and Dray (2018).
Introduction
Double constrained correspondence analysis (dc-CA) was developed as a natural extension of CCA and has been used to study the relationship between species traits and environmental variables.
In dc-CA, we have 3 matrices:
- A data matrix \(Y\) (\(r \times c\))
- A matrix of predictor variables \(E\) (\(r \times l\))
- A matrix of predictor variables \(T\) (\(c \times k\))
Code
dat <- readRDS(here("data/Barbaro2012.rds"))
Y <- dat$comm
E <- dat$envir
T_ <- dat$traits
r <- dim(Y)[1]
c <- dim(Y)[2]
l <- dim(E)[2]
k <- dim(T_)[2]
plotmat(r = r, c = c,
E = TRUE, T_ = TRUE,
l = l, k = k)
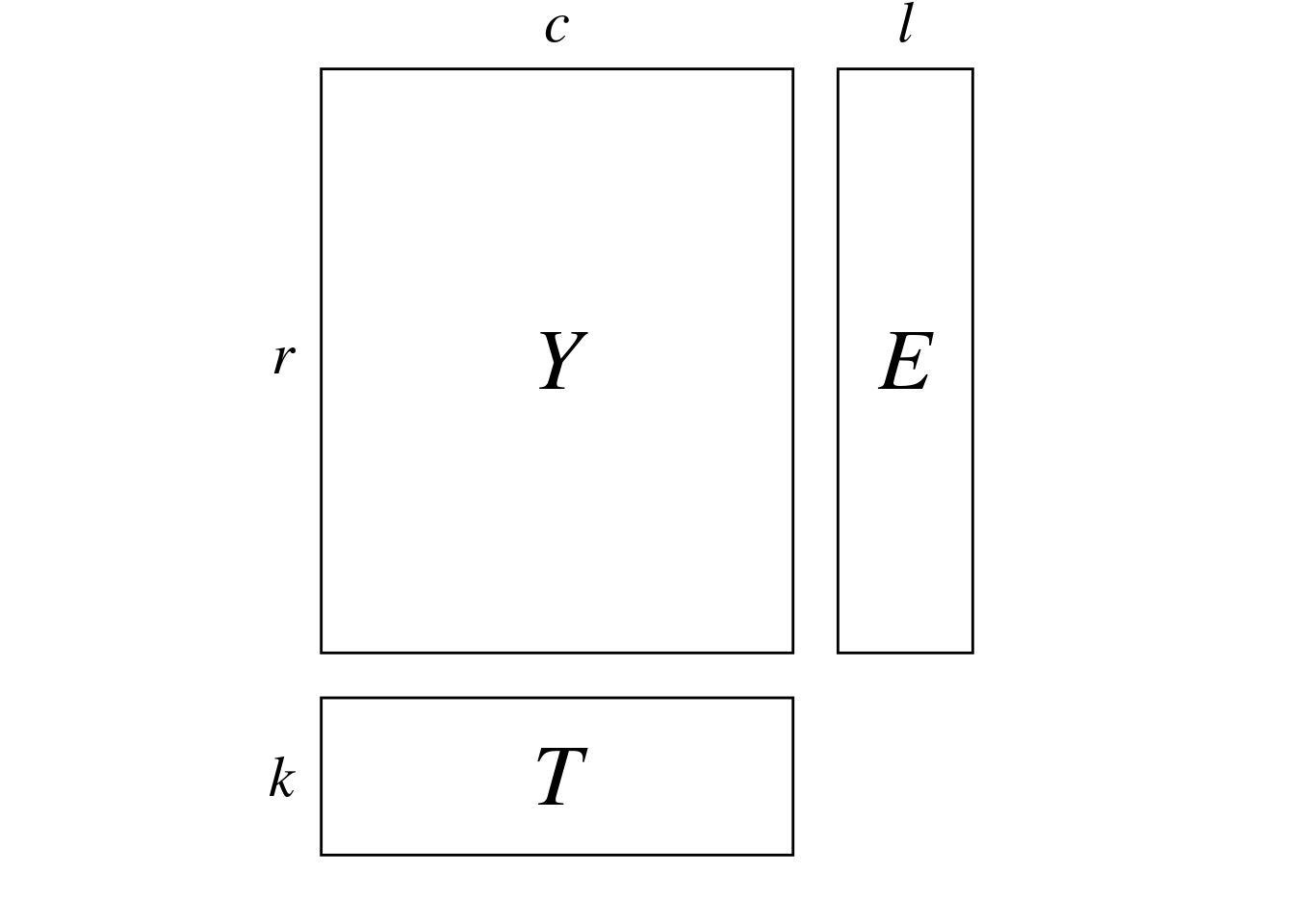
The aim of dc-CA is to find a linear combination of the predictor variables in \(E\) and \(T\) (environmental variables and traits) that maximizes the correlation.
Below are the first lines of these matrices for our data:
\(Y =\)
Code
knitr::kable(head(Y))| sp1 | sp2 | sp3 | sp4 | sp5 | sp6 | sp7 | sp8 | sp9 | sp10 | sp11 | sp12 | sp13 | sp14 | sp15 | sp16 | sp17 | sp18 | sp19 | sp21 | sp22 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 2 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 2 | 0 | 1 | 0 | 5 | 0 | 2 | 0 | 2 | 4 | 0 | 3 | 3 | 0 | 3 | 1 | 0 | 2 |
| 5 | 0 | 0 | 2 | 0 | 1 | 0 | 2 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 0 | 1 |
| 3 | 0 | 0 | 0 | 0 | 1 | 0 | 4 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 1 |
| 5 | 0 | 0 | 1 | 0 | 1 | 0 | 2 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 3 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 2 | 0 | 3 | 1 | 2 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 2 | 2 | 0 | 3 |
\(E =\)
Code
knitr::kable(head(E))| location | elevation | patch_area | perc_forests | perc_grasslands | ShannonLandscapeDiv |
|---|---|---|---|---|---|
| 0 | 10 | 6.28 | 7.7882 | 67.7785 | 0.232 |
| 0 | 30 | 7.92 | 16.4129 | 43.4066 | 0.274 |
| 0 | 430 | 83.24 | 24.4526 | 28.4995 | 0.274 |
| 0 | 420 | 140.83 | 41.9966 | 34.2412 | 0.260 |
| 0 | 400 | 140.83 | 41.9966 | 34.2412 | 0.260 |
| 0 | 500 | 0.50 | 7.5445 | 67.0780 | 0.240 |
\(T =\)
Code
knitr::kable(head(T_))| biog | forag | mass | diet | move | nest | eggs | |
|---|---|---|---|---|---|---|---|
| sp1 | 1 | 2 | 2 | 3 | 1 | 2 | 2 |
| sp2 | 1 | 1 | 1 | 2 | 1 | 2 | 2 |
| sp3 | 1 | 1 | 2 | 2 | 2 | 2 | 1 |
| sp4 | 1 | 1 | 1 | 2 | 1 | 2 | 2 |
| sp5 | 1 | 3 | 3 | 1 | 2 | 3 | 4 |
| sp6 | 1 | 1 | 4 | 3 | 2 | 2 | 1 |
(r <- dim(Y)[1])[1] 26(c <- dim(Y)[2])[1] 21(l <- dim(E)[2])[1] 6(k <- dim(T_)[2])[1] 7dc-CA must not have to many traits compared to species: that is a disadvantage compared to RLQ, but on the other hand dc-CA allows to see relationships that RLQ would miss (Braak, Šmilauer, and Dray 2018).
There are several ways to perform dc-CA (Braak, Šmilauer, and Dray 2018), notably:
- singular value decomposition (the method used here)
- an iterative method à la reciprocal averaging
- canonical correlation analysis between \(T\) et \(E\), weighted by \(P\)
Computation
TL;DR
We define matrix \(D\) as:
\[D = [\tilde{E}^\top D_r \tilde{E}]^{-1/2} \tilde{E}^\top P_0 \tilde{T} [\tilde{T}^\top D_c \tilde{T}]^{-1/2}\]
Note: contrary to Braak, Šmilauer, and Dray (2018), in this document we use the matrix \(P_0\) instead of \(Y\).
We perform the SVD of \(D\):
\[ D = B_0 \Delta C_0^\top \]
This allows us to find the eigenvectors \(B_0\) (regression coefficients multiplying rows/environment variables) and \(C_0\) (regression coefficients multiplying columns/species traits).
The eigenvalues of the dc-CA are the squared eigenvalues of the SVD: \(\Lambda = \Delta^2\).
There are \(\min(k, l)\) non-null eigenvalues???
Transformation of \(B_0\) and \(C_0\)
Then, we transform \(B_0\) and \(C_0\) (scaling):
- \(B = [\tilde{E}^\top D_r \tilde{E}]^{-1/2} B_0\) (coefficients for rows/environmental variables)
- \(C = [\tilde{T}^\top D_c \tilde{T}]^{-1/2} C_0\) (coefficients for columns/species traits)
Individuals coordinates
The individuals coordinates (species or sites) can be computed in two ways:
Linear combinations (LC scores) are computed from those coefficients :
- \(U = \tilde{E} B\) for the rows (sites)
- \(V = \tilde{T} C\) for columns (species)
Weighted averages (WA scores) are computed from the scores of the other individuals:
- \(U^\star = {D_r}^{-1} P_0 V\) for row (sites) scores
- \(V^\star = {D_c}^{-1} {P_0}^\top U\) for column (species) scores
Pre-computations
To check our results, we first perform a dc-CA with ade4:
ca <- dudi.coa(Y,
nf = c-1,
scannf = FALSE)
dcca <- dpcaiv2(dudi = ca,
dfR = E,
dfQ = T_,
scannf = FALSE,
nf = min(k, l))Center matrices
We define \(P\) as the relative counts of \(Y\) and \(P_0\) as its centered scaled version:
P <- Y/sum(Y)
# Initialize P0 matrix
P0 <- matrix(ncol = ncol(Y), nrow = nrow(Y))
colnames(P0) <- colnames(Y)
rownames(P0) <- rownames(Y)
for(i in 1:nrow(Y)) { # For each row
for (j in 1:ncol(Y)) { # For each column
# Do the sum
pi_ <- sum(P[i, ])
p_j <- sum(P[, j])
# Compute the transformation
P0[i, j] <- (P[i, j] - (pi_*p_j))/sqrt(pi_*p_j)
}
}First, we need to center-scale the traits and environment matrices (resp. \(\tilde{T}\) and \(\tilde{E}\)). To do so, we use the occurrences in matrix \(P\) as weights:
E_wt <- rowSums(P)/nrow(E)
Escaled <- scalewt(E, wt = E_wt, scale = TRUE)
T_wt <- colSums(P)/nrow(T_)
Tscaled <- scalewt(T_, wt = T_wt, scale = TRUE)# Check centering
M1 <- matrix(rep(1, nrow(P)), nrow = 1)
all(abs(M1 %*% diag(rowSums(P)) %*% Escaled) < zero)[1] TRUEM1 <- matrix(rep(1, ncol(P)), nrow = 1)
all(abs(M1 %*% diag(colSums(P)) %*% Tscaled) < zero)[1] TRUEThis is equivalent to scaling “inflated” versions of these matrices matching the occurrence counts in \(P\) (below).
\[ \tilde{E} = \frac{E - \bar{E}_{infl}}{\sigma_{Einfl}} \]
\[ \tilde{T} = \frac{T - \bar{T}_{infl}}{\sigma_{Tinfl}} \]
Code
# Center E -----
pi_ <- rowSums(P)
Escaled2 <- matrix(nrow = nrow(E), ncol = ncol(E))
for(i in 1:ncol(Escaled)) {
emean <- sum(E[, i]*pi_/sum(P))
Escaled2[, i] <- (E[, i] - emean)/(sqrt(sum(pi_*(E[, i] - emean)^2)))
}
# This is the same as computing a mean on inflated data matrix Einfl and centering E with these means
# Center T -----
p_j <- colSums(P)
Tscaled2 <- matrix(nrow = nrow(T_), ncol = ncol(T_))
rownames(Tscaled2) <- rownames(T_)
colnames(Tscaled2) <- colnames(T_)
for(j in 1:ncol(Tscaled)) {
tmean <- sum(T_[, j]*p_j/sum(P))
Tscaled2[, j] <- (T_[, j] - tmean)/(sqrt(sum(p_j*(T_[, j] - tmean)^2)))
}Code
# Check equivalence between the 2 methods
all(abs(Escaled/Escaled2 - 1) < zero)[1] TRUECode
all(abs(Tscaled/Tscaled2 - 1) < zero)[1] TRUERationale: regression
Then, we search scores \(u\) and \(v\) that maximize the fourth-corner correlation \(u^\top P v\) (where \(u\) are the sites (rows) scores and \(v\) are the species (columns) scores).
In this framework, we define \(u\) and \(v\) as linear combinations of traits and environmental variables: \(u = \tilde{E}b\) and \(v = \tilde{T}c\).
So in the end, we need to maximize \(u^\top P_0 v\) with respect to the coefficients vectors \(b\) and \(c\):
\[ \max_{b, c}(u^\top P v) = \max_{b, c}\left(\left[\tilde{E}b\right]^\top P \tilde{T}c \right) \]
Note
These equations are written for the first axis, but we can also write them in matrix form:
\[ \max_{B, C}(U^\top P V) = \max_{B, C}\left(\left[\tilde{E}B\right]^\top P \tilde{T}C \right) \]
We define the diagonal matrices \(D_r\) and \(D_c\), which contain the column and row sums of \(P\) (respectively). We introduce the following constraint on \(U\) and \(V\): \(u^\top D_r u = 1\) and \(v^\top D_c v = 1\). It means that the matrices \(U\) and \(V\) are orthonormal with respect to the weights \(D_r\) and \(D_c\). (In fact, these constraints will be relaxed later depending on the scaling (see below)).
To find the coefficients \(B\) and \(C\) defined above, we can perform a SVD or two diagonalizations (see below).
SVD
To find the coefficients \(B\) and \(C\), we perform the SVD of a matrix \(D\) defined as:
\[ D = \underbrace{[\tilde{E}^\top D_r \tilde{E}]^{-1/2}}_{L^{-1/2}} \underbrace{\tilde{E}^\top P \tilde{T}}_{R} \underbrace{[\tilde{T}^\top D_c \tilde{T}]^{-1/2}}_{K^{-1/2}} \]
# Define weights
dr <- rowSums(P)
dc <- colSums(P)
Dr <- diag(dr)
Dc <- diag(dc)# Define intermediate matrices
L <- t(Escaled) %*% Dr %*% Escaled
R <- t(Escaled) %*% P %*% Tscaled
K <- t(Tscaled) %*% Dc %*% TscaledWith our dataset:
D <- solve(sqrtm(t(Escaled) %*% Dr %*% Escaled)) %*%
t(Escaled) %*% P %*% Tscaled %*%
solve(sqrtm(t(Tscaled) %*% Dc %*% Tscaled))We perform the SVD of \(D\):
\[D = B_0 \Delta C_0^\top\]
sv <- svd(D)
# Singular values
delta <- sv$d
Delta <- diag(delta)
# Eigenvalues
lambda <- delta^2
Lambda <- diag(lambda)
# Eigenvectors
B0 <- sv$u
dim(B0) # l x l[1] 6 6C0 <- sv$v
dim(C0) # k x l[1] 7 6Diagonalizations
Equivalently, we can also diagonalize the matrices \(M\) and \(M_2\) defined below.
\(M\) is defined as:
\[ M = [\underbrace{\tilde{E}^\top D_r \tilde{E}}_{L} ]^{-1} \underbrace{\tilde{E}^\top P \tilde{T}}_{R} [ \underbrace{\tilde{T}^\top D_c \tilde{T}}_{K} ]^{-1} \underbrace{\tilde{T}^\top P^\top \tilde{E}}_{R^\top} \tag{1}\]
We can also view \(M\) as:
\[ M = \underbrace{\left[\tilde{E}^\top D_r \tilde{E} \right]^{-1} \tilde{E}^\top P \tilde{T}}_{\hat{E}_{center} = \beta \tilde{T}} \underbrace{\left[\tilde{T}^\top D_c \tilde{T} \right]^{-1} \tilde{T}^\top P^\top \tilde{E}}_{\hat{T}_{center} = \gamma \tilde{E}} \]
where \(\hat{E}_{center}\) is the predicted values of sites variables from species traits. Reciprocally, \(\hat{T}_{center}\) is the predicted values of species traits from sites variables. \(\beta\) and \(\gamma\) are the vectors of the regression coefficients. From Equation 1, we have \(\beta = \left[\tilde{E}^\top D_r \tilde{E} \right]^{-1} \tilde{E}^\top P\) and \(\gamma = \left[\tilde{T}^\top D_c \tilde{T} \right]^{-1} \tilde{T}^\top P^\top\).
M <- solve(t(Escaled) %*% Dr %*% Escaled) %*% t(Escaled) %*% P %*% Tscaled %*% solve(t(Tscaled) %*% Dc %*% Tscaled) %*% t(Tscaled) %*% t(P) %*% Escaled\(M_2\) is defined as:
\[ M_2 = \underbrace{\left[\tilde{T}^\top D_c \tilde{T} \right]^{-1} \tilde{T}^\top P^\top \tilde{E}}_{\hat{T}_{center} = \gamma \tilde{E}} \underbrace{\left[\tilde{E}^\top D_r \tilde{E} \right]^{-1} \tilde{E}^\top P \tilde{T}}_{\hat{E}_{center} = \beta \tilde{T}} \]
M2 <- solve(t(Tscaled) %*% Dc %*% Tscaled) %*% t(Tscaled) %*% t(P) %*% Escaled %*% solve(t(Escaled) %*% Dr %*% Escaled) %*% t(Escaled) %*% P %*% Tscaled The eigenvectors matrices of these diagonalizations give us \(B\) and \(C\):
- To find \(B\), we diagonalize \(M\):
\[ M = B \Lambda_b B^{-1} \]
# Diagonalize M
eigB <- eigen(M)
lambdaB <- eigB$values
lambdaB # All l = 6 non-null eigenvectors[1] 0.139487442 0.088736680 0.049183623 0.013797529 0.008736645 0.002485683B_diag <- eigB$vectors
# Check that the result checks out with SVD
all(abs(abs(B_diag/B0) - 1) < zero) # it isn't equal[1] FALSEapply(B_diag, 2, function(x) sqrt(sum(x^2))) # but B_diag is of norm 1 (like B0)[1] 1 1 1 1 1 1- Similarly, to find \(C\), we must diagonalize \(M_2\):
\[ M_2 = C \Lambda_c C^{-1} \]
# Diagonalize M2
eigC <- eigen(M2)
lambdaC <- eigC$values
lambdaC # l = 6 non-null eigenvalues[1] 1.394874e-01 8.873668e-02 4.918362e-02 1.379753e-02 8.736645e-03
[6] 2.485683e-03 -1.180064e-17C_diag <- eigC$vectors
# Check that the result checks out with SVD
all(abs(abs(C_diag[, 1:l]/C0) - 1) < zero) # it isn't equal[1] FALSEapply(C_diag[, 1:l], 2, function(x) sqrt(sum(x^2))) # but C_diag is of norm 1 (like C0)[1] 1 1 1 1 1 1# The two diagonalizations have the same non-null eigenvectors
all(lambdaB - lambdaC[1:l] < zero)[1] TRUEThe eigenvalues of the SVD \(\Lambda = \Delta^2\) are the same as \(\Lambda_b\) and \(\Lambda_c\).
all(abs(lambda - lambdaB) < zero)[1] TRUECompute \(B\) and \(C\)
We also define the following “scalings” for the coefficients:
\[ \left\{ \begin{array}{ll} B &= L^{-1/2} B_0\\ C &= K^{-1/2} C_0 \end{array} \right. \]
(We recall that \(L = \tilde{E}^\top D_r \tilde{E}\) and \(K = \tilde{T}^\top D_c \tilde{T}\)).
B <- solve(sqrtm(L)) %*% B0
C <- solve(sqrtm(K)) %*% C0# B0 and C0 are of norm 1
apply(B0, 2, function(x) sqrt(sum(x^2))) [1] 1 1 1 1 1 1apply(C0, 2, function(x) sqrt(sum(x^2))) [1] 1 1 1 1 1 1# B and C are normed with L and K
# t(B) L B is the identity matrix
id_l <- diag(1, nrow = l, ncol = l)
all(abs((t(B) %*% L %*% B) - id_l) < zero)[1] TRUE# t(C) K C is the identity matrix
id_c <- diag(c(rep(1, k-1), 0),
nrow = k, ncol = k) # Identity minus last vector (zero)
C_k <- cbind(C, rep(0, k)) # Add null eigenvector
all(abs(t(C_k) %*% K %*% C_k - id_c) < zero)[1] TRUESites and species scores
LC scores
Using the coefficients \(B\) and \(C\), we can now define scores for sites and species scores as a linear combination of their variables:
- sites scores predicted by environmental variables are \(U = \tilde{E} B\)
U <- Escaled %*% B0
# Check it is the same as ade4 scores
all(abs(U/dcca$l1) - 1 < zero)[1] FALSE- species scores predicted by their traits are \(V = \tilde{T} C\)
V <- Tscaled %*% C
# Check it is the same as ade4 scores
all(abs(V/dcca$c1) - 1 < zero)[1] TRUEWA scores
We can also define species scores as the mean of sites LC scores (and the reverse):
- sites scores as weighted averages of species scores are \(U^\star = D_r^{-1} P V\)
Ustar <- solve(Dr) %*% P %*% V
# Check it is the same as ade4 scores
all(abs(Ustar/dcca$lsR) - 1 < zero)[1] TRUE- species scores as weighted averages of sites scores are \(V^\star = D_c^{-1} P^\top U\)
Vstar <- solve(Dc) %*% t(P) %*% U
# Check it is the same as ade4 scores
all(abs(Vstar/dcca$lsQ) - 1 < zero)[1] FALSEScalings
TL;DR
There are two types of coordinates: linear combination scores (LC scores) and weighted averages scores (WA scores) for the sites and species individuals.
The general formulas are:
- the LC scores for rows (sites) are \(U_i = \tilde{E} B \Lambda^{\alpha/2}\)
- the LC scores for columns (species) are \(V_i = \tilde{T}C_i \Lambda^{(1 - \alpha)/2}\)
- the WA scores for rows (sites) are \(U^\star_i = {D_r}^{-1} P V_i\)
- the WA scores for columns (species) are \(V^\star_i = {D_c}^{-1} P^\top U_i\)
- the correlations with axes for the rows (environmental variables) are \(BS_{Bi} = B \Lambda^{\alpha/2}\)
- the correlations with axes for the columns (species traits) are \(BS_{Ci} = C \Lambda^{(\alpha - 1)/2}\)
In these formulas, note that the WA scores for one dimension are computed from the predicted scores of the other dimension.
Scaling type 1 (\(\alpha = 1\))
- the LC scores for rows (sites) are \(U_1 = \tilde{E} B \Lambda^{1/2}\) (
li) - the LC scores for columns (species) are \(V_1 = \tilde{T}C\) (
c1) - the WA scores for rows (sites) are \(U^\star_1 = {D_r}^{-1} P V_1\) (
lsR) - the WA scores for columns (species) are \(V^\star_1 = {D_c}^{-1} P^\top U_1\)
- the correlations with axes for the rows (environmental variables) are \(BS_{B1} = B \Lambda^{1/2}\)
- the correlations with axes for the columns (species traits) are \(BS_{C1} = C\)
Scaling type 2 (\(\alpha = 0\))
- the LC scores for rows (sites) are \(U_2 = \tilde{E} B\) (
l1) - the LC scores for columns (species) are \(V_2 = \tilde{T}C \Lambda^{1/2}\) (
co) - the WA scores for rows (sites) are \(U^\star_2 = {D_r}^{-1} P V_2\)
- the WA scores for columns (species) are \(V^\star_2 = {D_c}^{-1} P^\top U_2\) (
lsQ) - the correlations with axes for the rows (environmental variables) are \(BS_{B2} = B\)
- the correlations with axes for the columns (species traits) are \(BS_{C2} = C \Lambda^{1/2}\)
Scaling type 3 (\(\alpha = 1/2\))
- the LC scores for rows (sites) are \(U_3 = \tilde{E} B \Lambda^{1/4}\)
- the LC scores for columns (species) are \(V_3 = \tilde{T} C \Lambda^{1/4}\)
- the WA scores for rows (sites) are \(U^\star_3 = {D_r}^{-1} P V_3\)
- the WA scores for columns (species) are \(V^\star_3 = {D_c}^{-1} P^\top U_3\)
- the correlations with axes for the rows (environmental variables) are \(BS_{B3} = B \Lambda^{1/4}\)
- the correlations with axes for the columns (species traits) are \(BS_{C3} = C \Lambda^{1/4}\)
\(\alpha\) changes the interpretation of the correlations vectors:
- the following vectors are used for intra-set correlations: \(BS_{B2}\) (\(\alpha = 0\)), to approximate the correlations between the environmental/row variables and the sites, and \(BS_{C1}\) (\(\alpha = 1\)) for the correlations between the traits/column variables and the species.
- inter-set correlations (fourth-corner): \(BS_{B1}\) (\(\alpha = 1\)) approximates the correlation between environmental/row variables and columns/species and \(BS_{C2}\) (\(\alpha = 0\)) approximates the correlation between columns variables/traits and sites.
- \(BS_{B3}\) and \(BS_{C3}\) (\(\alpha = 1/2\)) is the geometric mean of scalings 1 and 2.
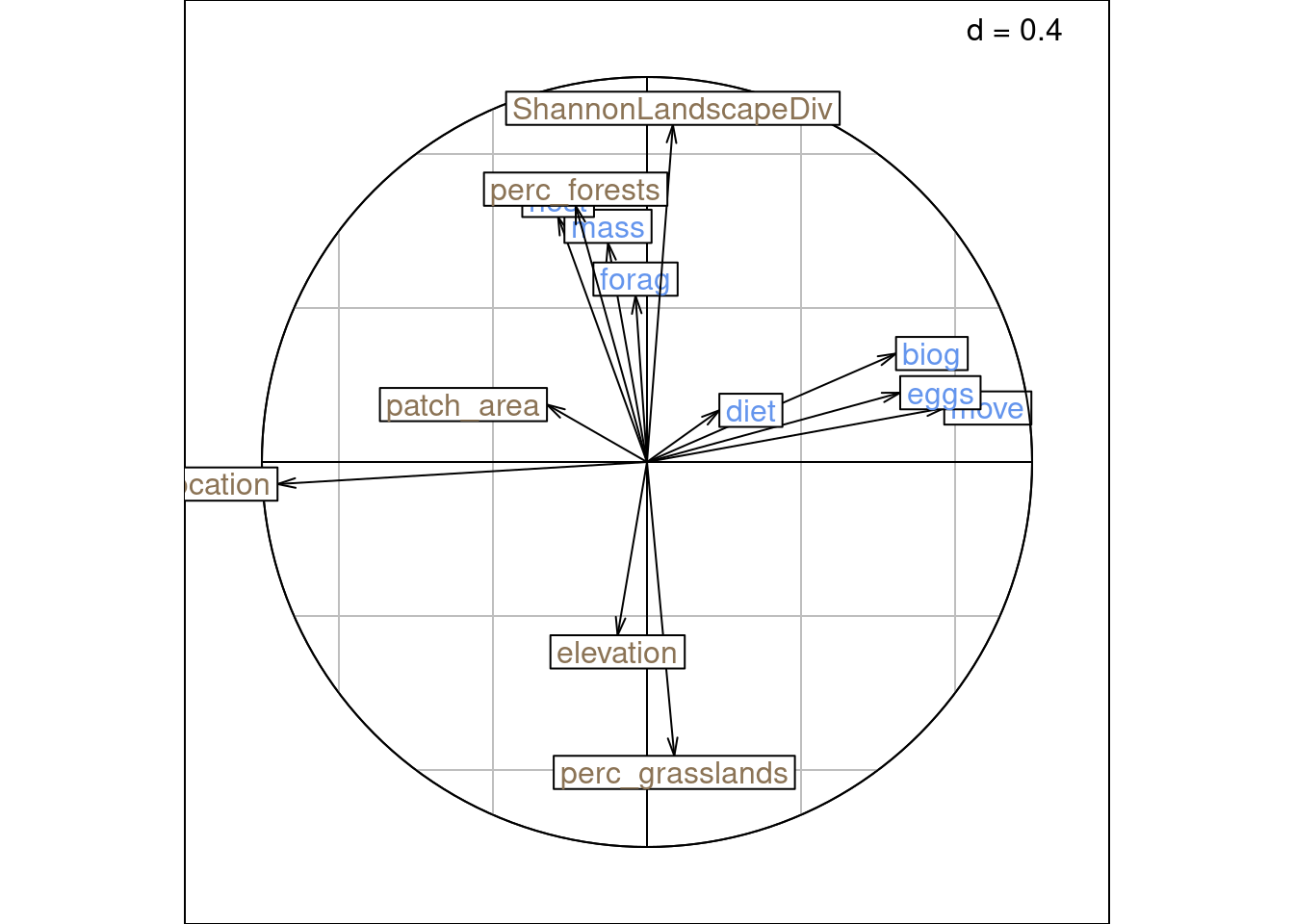
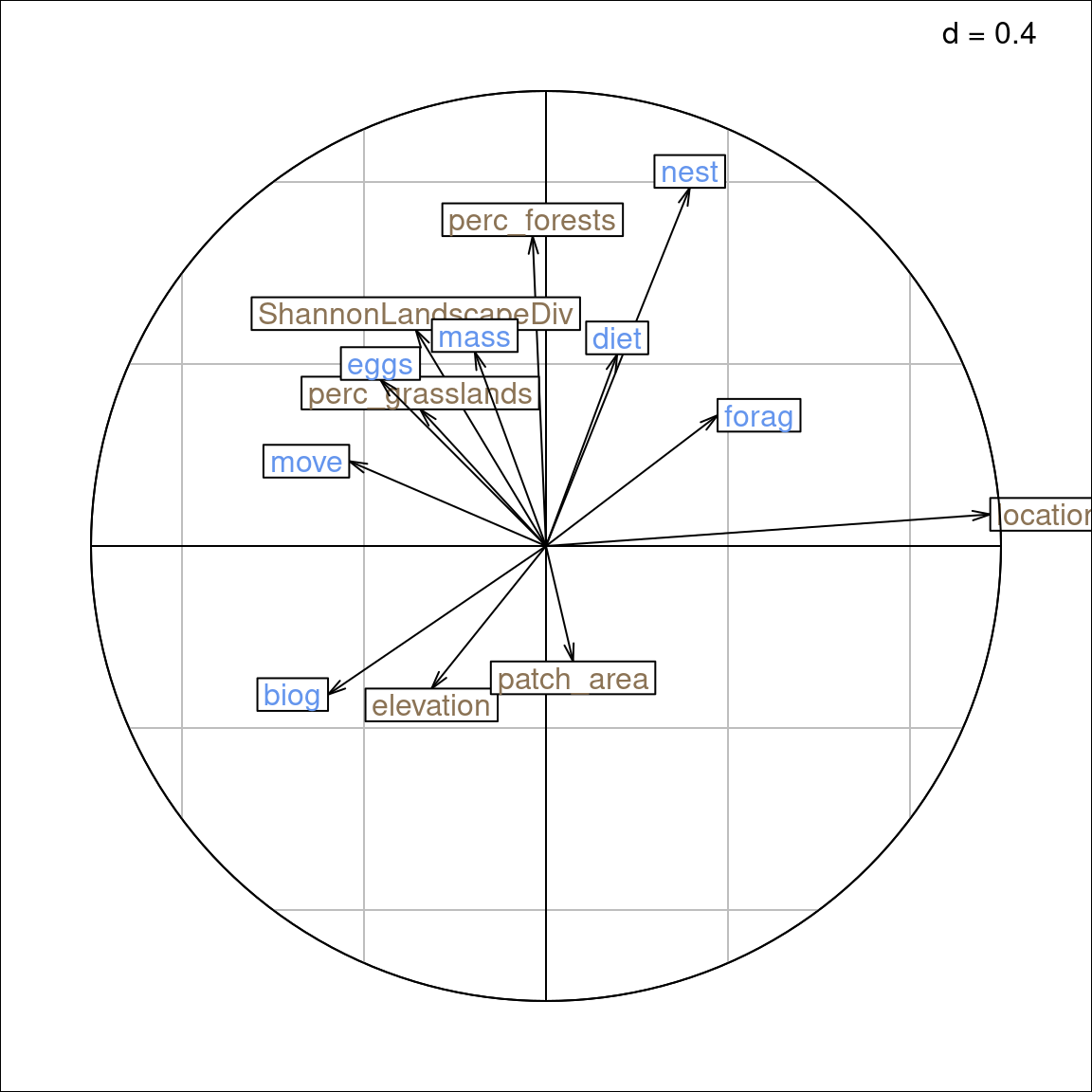
When plotting the correlation circle, to look at the correlations between variables of the same set (traits or environmental variables), we should use \(BS_{B2}\) and \(BS_{C1}\). There are the scores returned by ade4.
Scaling type 1
This type of scaling preserves the distances between rows (\(\alpha = 1\)).
- the rows (sites) scores can be \(U^\star_1\) (WA scores) or \(U_1\) (LC scores)
- the columns (species) scores can be \(V^\star_1\) (WA scores) or \(V_1\) (LC scores)
- rows variables (environmental variables) correlations are \(BS_{B1}\).
- columns variables (species traits) correlations are \(BS_{C1}\)
With the scaling type 1, \(BS_{B1}\) represents the correlation between environmental variables and species and \(BS_{C1}\) represents the correlation between species traits and species.
# LC scores
U1 <- Escaled %*% B %*% Delta # rows
V1 <- Tscaled %*% C # columns
# WA scores
Ustar1 <- solve(Dr) %*% P %*% V # rows
Vstar1 <- solve(Dc) %*% t(P) %*% U # columns
# # Variables scores
BS_B1 <- B %*% Delta
BS_C1 <- C
# Normalize
BS_B1norm <- normalize(BS_B1, 1)
BS_C1norm <- normalize(BS_C1, 1)
BS_C1 <- t(Tscaled) %*% Dc %*% V# Compare results to ade4
all(abs(U1/dcca$li) - 1 < zero) # sites LC[1] TRUEall(abs(V1/dcca$c1) - 1 < zero) # spp LC[1] TRUEall(abs(Ustar1/dcca$lsR) - 1 < zero) # sites WA[1] TRUEall(abs(abs(Vstar1/dcca$lsQ) - 1) < zero) # not stored in ade4[1] FALSEall(abs(abs(BS_C1/dcca$corQ) - 1) < zero)[1] TRUEPlots
We can either plot:
- sites as \(U_1\) (
li) and species as \(V_1\) (c1) (left) - sites as \(U^\star_1\) (
lsR) and species as \(V_1\) (c1) (right)
Code
# LC scores
glc <- multiplot(indiv_row = U1, # LC for sites
indiv_col = V1, # LC1 for spp
indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y),
# var_row = BS_B1norm, var_row_lab = colnames(E),
# var_col = BS_C1norm, var_col_lab = colnames(T_),
row_color = params$colsite, col_color = params$colspp,
eig = lambda) +
ggtitle("Sites LC scores with species\nnormed at 1")
# WA scores
gwa <- multiplot(indiv_row = Ustar1, # WA for sites
indiv_col = V1, # LC1 for spp
indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y),
# var_row = BS_B1norm, var_row_lab = colnames(E),
# var_col = BS_C1norm, var_col_lab = colnames(T_),
row_color = params$colsite, col_color = params$colspp,
eig = lambda) +
ggtitle("Sites WA scores with species\nnormed at 1")
glc + gwa +
plot_layout(axis_titles = "collect")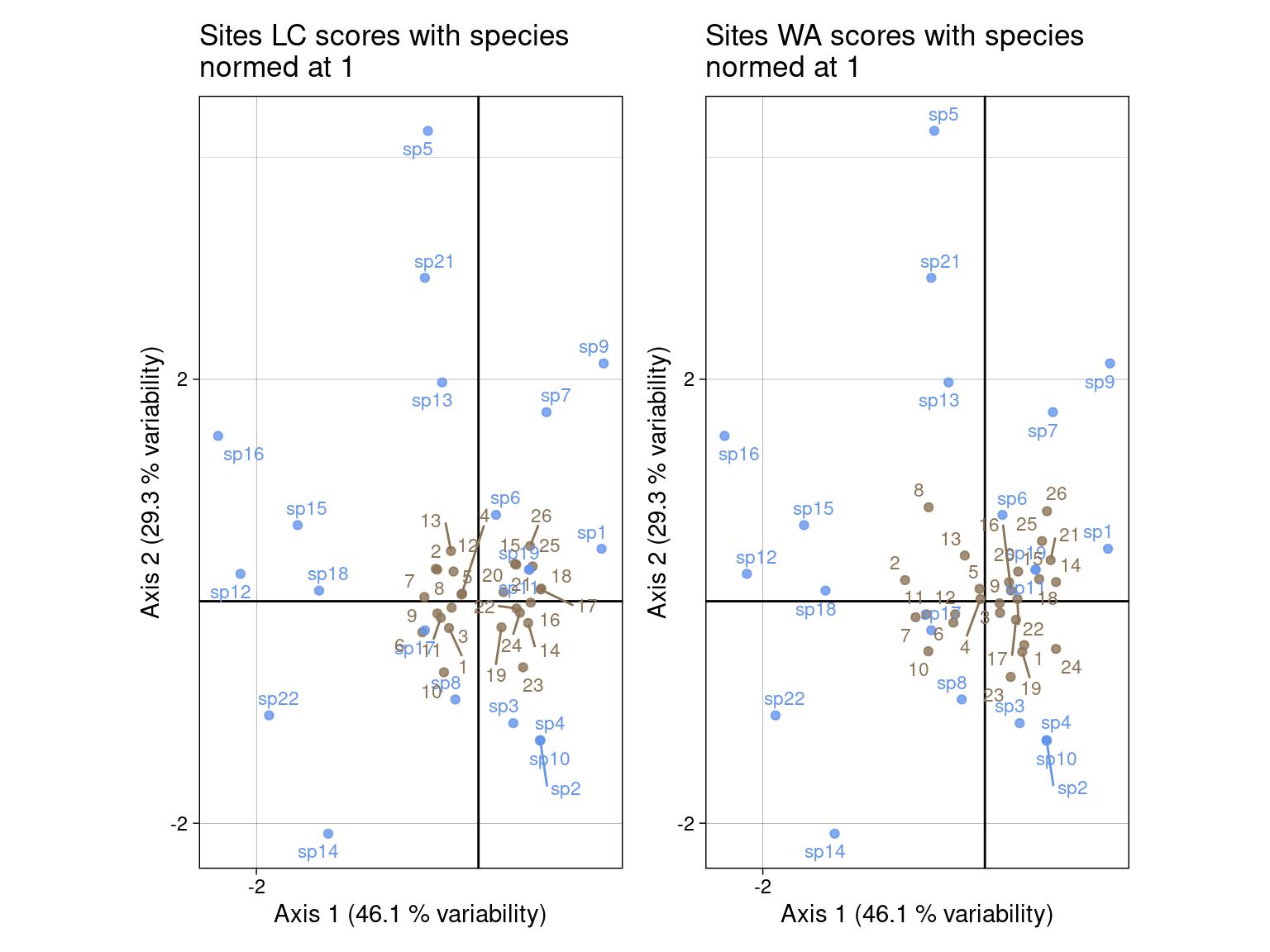
Code
s.corcircle(BS_B1norm,
labels = colnames(E),
plabels.col = params$colsite)
s.corcircle(BS_C1norm,
labels = colnames(T_),
plabels.col = params$colspp, add = TRUE)
On this plot, we can interpret 5 sets of pairs:
- row and columns variables (\(BS_{B1}\) - \(BS_{C1}\)): angles between arrows of rows and environmental variables represent their fourth-corner correlation. For instance, the correlation between
massandperc_forestsis large (arrows size + direction). - species and environmental variables (\(BS_{B1}\) - \(V\)): species points on the right (e.g. sp1) are located in sites with a high
locationvariable. - sites and species traits (\(BS_{C1}\) - \(U\)): we can understand sites using their community weighted mean (eg site 26 has birds with high mass).
- species and species traits (\(BS_{C1}\) - \(U\)): for instance, species 12 has large eggs.
The last pair is the individuals on each plot:
- On the first plot (with sites LC scores), \(U_1\) and \(V_1\) form a biplot of contingency ratio (Braak, Šmilauer, and Dray 2018)
- On the second plot (with sites WA scores), \(U^\star_1\) is placed at the mean of \(V_1\).
Moreover, species traits (\(BS_C^1\)): arrows indicate intra-set correlations.
There is no interpretation for sites - environmental variables (\(U_1\) - \(BS_{B1}\)).
Same plots with ade4:
Code
s.label(dcca$c1, # Species LC1
plabels.optim = TRUE,
plabels.col = params$colspp,
ppoints.col = params$colspp,
main = "LC scores for sites")
s.label(dcca$li, # Sites LC
plabels.optim = TRUE,
plabels.col = params$colsite,
ppoints.col = params$colsite,
add = TRUE)
Code
s.label(dcca$c1, # Species LC1
plabels.optim = TRUE,
plabels.col = params$colspp,
ppoints.col = params$colspp,
main = "WA scores for sites")
s.label(dcca$lsR, # Sites WA scores
plabels.optim = TRUE,
plabels.col = params$colsite,
ppoints.col = params$colsite,
add = TRUE)
Code
s.corcircle(dcca$corQ,
plabels.col = params$colspp)
s.corcircle(dcca$corR,
plabels.col = params$colsite, add = TRUE)
Scaling type 2
This type of scaling preserves the distances between columns.
- the rows (sites) scores can be \(U^\star_2\) (WA scores) or \(U_2\) (LC scores)
- the columns (species) scores can be \(V^\star_2\) (WA scores) or \(V_2\) (LC scores)
- rows variables (environmental variables) correlations are \(BS_{B2}\).
- columns variables (species traits) correlations are \(BS_{C2}\)
With the scaling type 2, \(BS_{B2}\) represents the correlation between environmental variables and sites and \(BS_{C2}\) represents the correlation between species traits and sites.
# LC scores
U2 <- Escaled %*% B # rows
V2 <- Tscaled %*% C %*% Delta # columns
# WA scores
Ustar2 <- solve(Dr) %*% P %*% V2 # rows
Vstar2 <- solve(Dc) %*% t(P) %*% U2 # columns
# Variables scores
BS_B2 <- t(Escaled) %*% Dr %*% U2
# BS_B2 <- B
# BS_C2 <- C %*% Delta
#
# # Normalize
# BS_B2norm <- normalize(BS_B2, 1)
# BS_C2norm <- normalize(BS_C2, 1)all(abs(U2/dcca$l1) - 1 < zero) # LC sites[1] TRUEall(abs(V2/dcca$co) - 1 < zero) # LC spp[1] TRUEall(abs(Vstar2/dcca$lsQ) - 1 < zero) # WA spp[1] TRUEall(abs(Ustar2/dcca$lsR) - 1 < zero) # WA site[1] TRUEall(abs(abs(BS_B2/dcca$corR) - 1) < zero)[1] TRUEPlots
We can either plot:
- sites as \(U_2\) (
l1) and species as \(V_2\) (co) (left) - sites as \(U_2\) (
l1) and species as \(V^\star_2\) (lsQ) (right)
Code
# LC scores
glc <- multiplot(indiv_row = U2, indiv_col = V2,
indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y),
# var_row = BS_B2norm, var_row_lab = colnames(E),
# var_col = BS_C2norm, var_col_lab = colnames(T_),
row_color = params$colsite, col_color = params$colspp,
eig = lambda) +
ggtitle("Species LC scores with sites\nnormed at 1")
# WA scores
gwa <- multiplot(indiv_row = U2, indiv_col = Vstar2,
indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y),
# var_row = BS_B2norm, var_row_lab = colnames(E),
# var_col = BS_C2norm, var_col_lab = colnames(T_),
row_color = params$colsite, col_color = params$colspp,
eig = lambda) +
ggtitle("Species WA scores with sites\nnormed at 1")
glc + gwa +
plot_layout(axis_titles = "collect")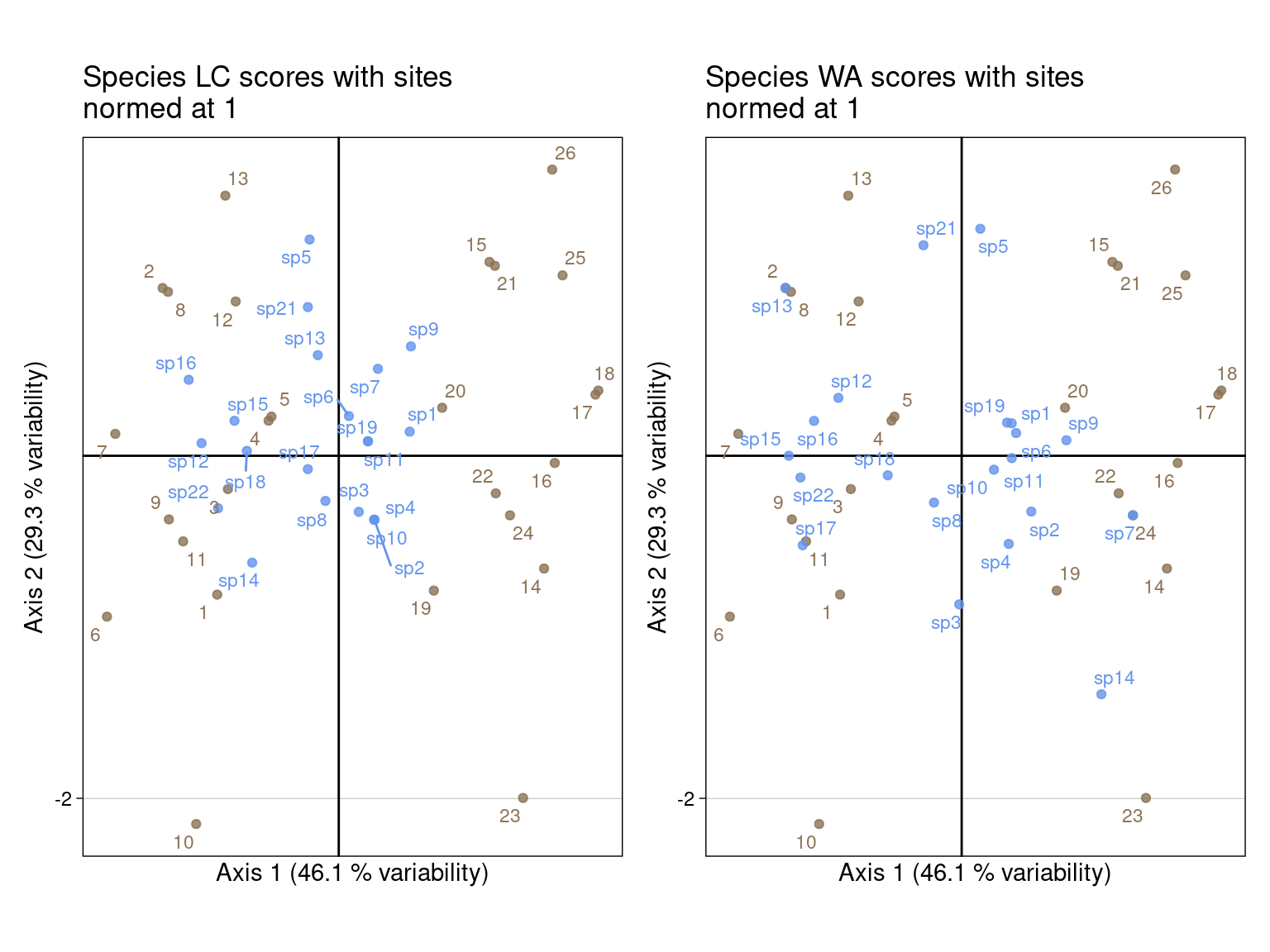
Code
# s.corcircle(BS_B2norm,
# labels = colnames(E),
# plabels.col = params$colsite)
# s.corcircle(BS_C2norm,
# labels = colnames(T_),
# plabels.col = params$colspp, add = TRUE)There is no interpretation for species - species traits (\(V_2\) - \(BS_{C2}\)).
With ade4:
Code
s.label(dcca$li, # LC1 sites
plabels.optim = TRUE,
plabels.col = params$colsite,
ppoints.col = params$colsite,
main = "LC scores for species")
s.label(dcca$co, # LC species
plabels.optim = TRUE,
plabels.col = params$colspp,
ppoints.col = params$colspp,
add = TRUE)
Code
s.label(dcca$l1, # LC1 sites
plabels.optim = TRUE,
plabels.col = params$colsite,
ppoints.col = params$colsite,
main = "WA scores for species")
s.label(dcca$lsQ, # WA species
plabels.optim = TRUE,
plabels.col = params$colspp,
ppoints.col = params$colspp,
add = TRUE)
Scaling type 3
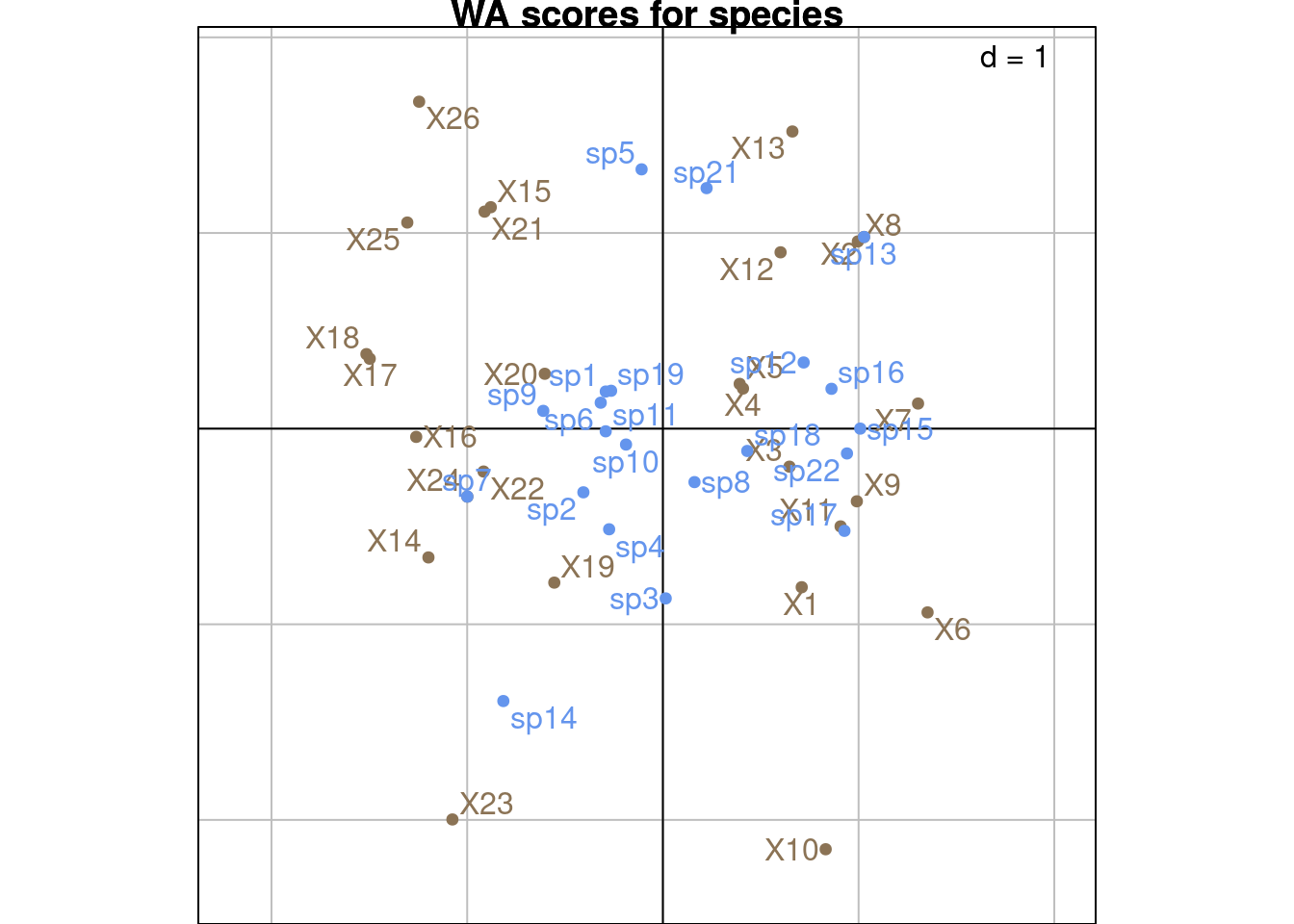
This type of scaling is an intermediate between scalings 1 and 2.
- the rows (sites) scores can be \(U^\star_3\) (WA scores) or \(U_3\) (LC scores)
- the columns (species) scores can be \(V^\star_3\) (WA scores) or \(V_3\) (LC scores)
- rows variables (environmental variables) correlations are \(BS_{B3}\).
- columns variables (species traits) correlations are \(BS_{C3}\)
With the scaling type 3, \(BS_{B3}\) and \(BS_{C3}\) represent the geometric mean of their correlation with species and sites.
# LC scores
U3 <- Escaled %*% B %*% Delta^(1/2) # rows
V3 <- Tscaled %*% C %*% Delta^(1/2) # columns
# WA scores
Ustar3 <- solve(Dr) %*% P %*% V3 # rows
Vstar3 <- solve(Dc) %*% t(P) %*% U3 # columns
# Variables scores
BS_B3 <- B %*% Delta^(1/2)
BS_C3 <- C %*% Delta^(1/2)
# Normalize
BS_B3norm <- normalize(BS_B3, 1)
BS_C3norm <- normalize(BS_C3, 1)Plots
Code
# LC scores
glc <- multiplot(indiv_row = U3, indiv_col = V3,
indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y),
# var_row = BS_B3norm, var_row_lab = colnames(E),
# var_col = BS_C3norm, var_col_lab = colnames(T_),
row_color = params$colsite, col_color = params$colspp,
eig = lambda) +
ggtitle("LC scores")
# WA scores
gwa <- multiplot(indiv_row = Ustar3, indiv_col = Vstar3,
indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y),
# var_row = BS_B3norm, var_row_lab = colnames(E),
# var_col = BS_C3norm, var_col_lab = colnames(T_),
row_color = params$colsite, col_color = params$colspp,
eig = lambda) +
ggtitle("WA scores")
glc + gwa +
plot_layout(axis_titles = "collect")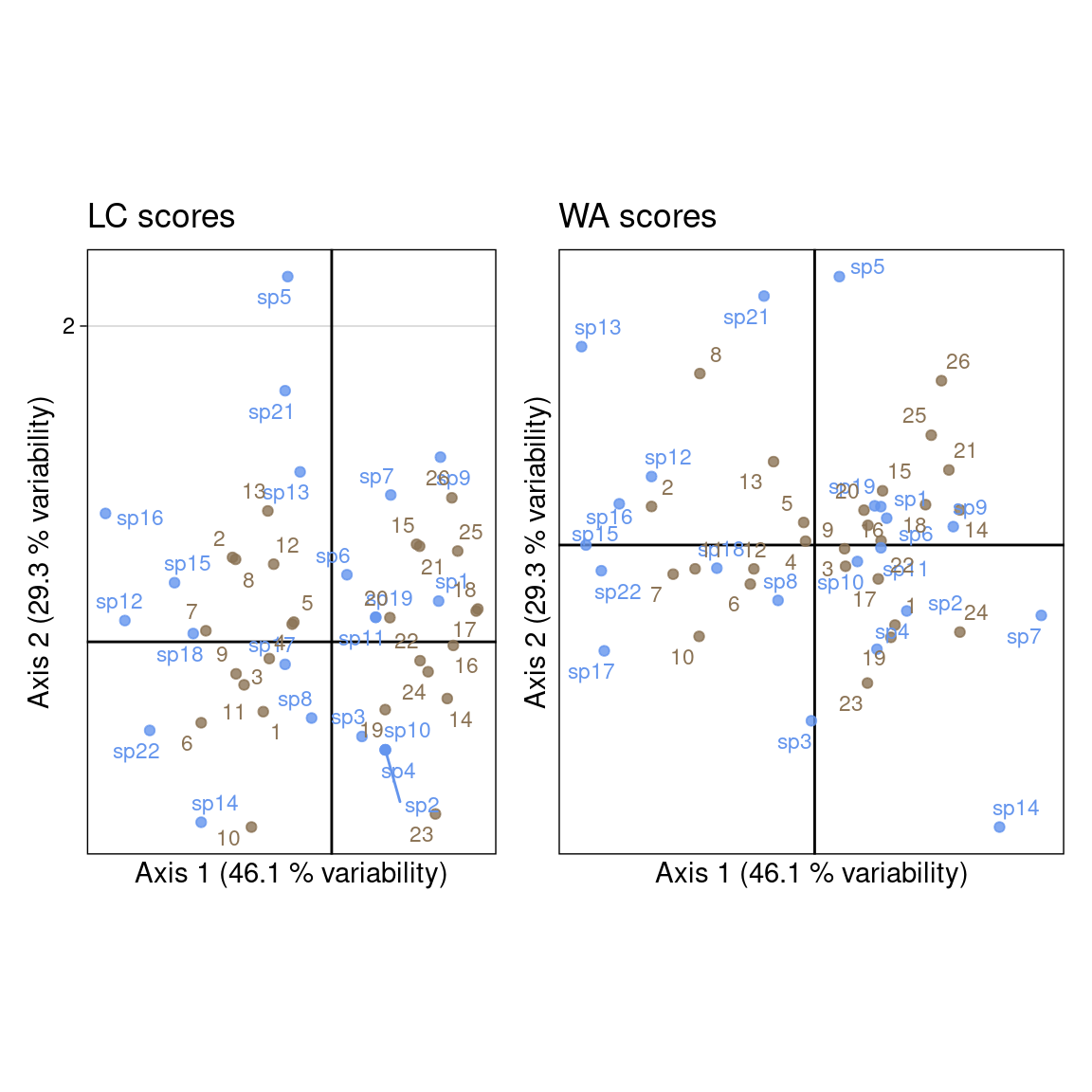
Code
s.corcircle(BS_B3norm,
labels = colnames(E),
plabels.col = params$colsite)
s.corcircle(BS_C3norm,
labels = colnames(T_),
plabels.col = params$colspp, add = TRUE)
Interpretation
This method finds the linear correlation of row explanatory variables (environmental variables) and the linear correlation of columns explanatory variables (species traits) that maximizes the fourth-corner correlation, i.e. the correlation between these linear combinations of row and columns-variables.
There are other related methods, that have been better described and also more used in ecology: RLQ, community weighted means RDA (CMW-RDA).
Contrary to RLQ, dc-CA takes into account the correlation between the row and column variables. Thus, while RLQ can analyze any number of row and column variables, it is not the case with dc-CA the number of row and column variables must not be large compared to the number of rows/columns in the tables. Also, dc-CA maximizes correlation and RLQ maximizes covariance (Braak, Šmilauer, and Dray 2018).
The eigenvalues of dc-CA are the squares of the fourth-corner correlations.
References
Braak, Cajo J. F. ter, Petr Šmilauer, and Stéphane Dray. 2018. “Algorithms and Biplots for Double Constrained Correspondence Analysis.” Environmental and Ecological Statistics 25 (2): 171–97. https://doi.org/10.1007/s10651-017-0395-x.