Canonical Correspondence Analysis (CCA)

Code

# Paths
library(here)

# Multivariate analysis
library(ade4)
library(adegraphics)

# Matrix algebra
library(expm)

# Plots
library(ggplot2)
library(CAnetwork)
library(patchwork)

Code

# Define bound for comparison to zero
zero <- 10e-10

The contents of this page relies heavily on Legendre and Legendre (2012).

Introduction

CCA is a method of the family of canonical or direct gradient analyses, in which a matrix of predictor variables intervenes in the computation of the ordination vectors.

CCA is an asymmetric method because the predictor variables and the response variables are not equivalent in the analysis.

CCA takes two matrices in input:

A data matrix \(Y\) (\(r \times c\))
A matrix of predictor variables \(E\) (\(r \times l\))

Code

dat <- readRDS(here("data/Barbaro2012.rds"))
Y <- dat$comm
E <- dat$envir

r <- dim(Y)[1]
c <- dim(Y)[2]
l <- dim(E)[2]

plotmat(r = r, c = c, l = l, 
        E = TRUE)

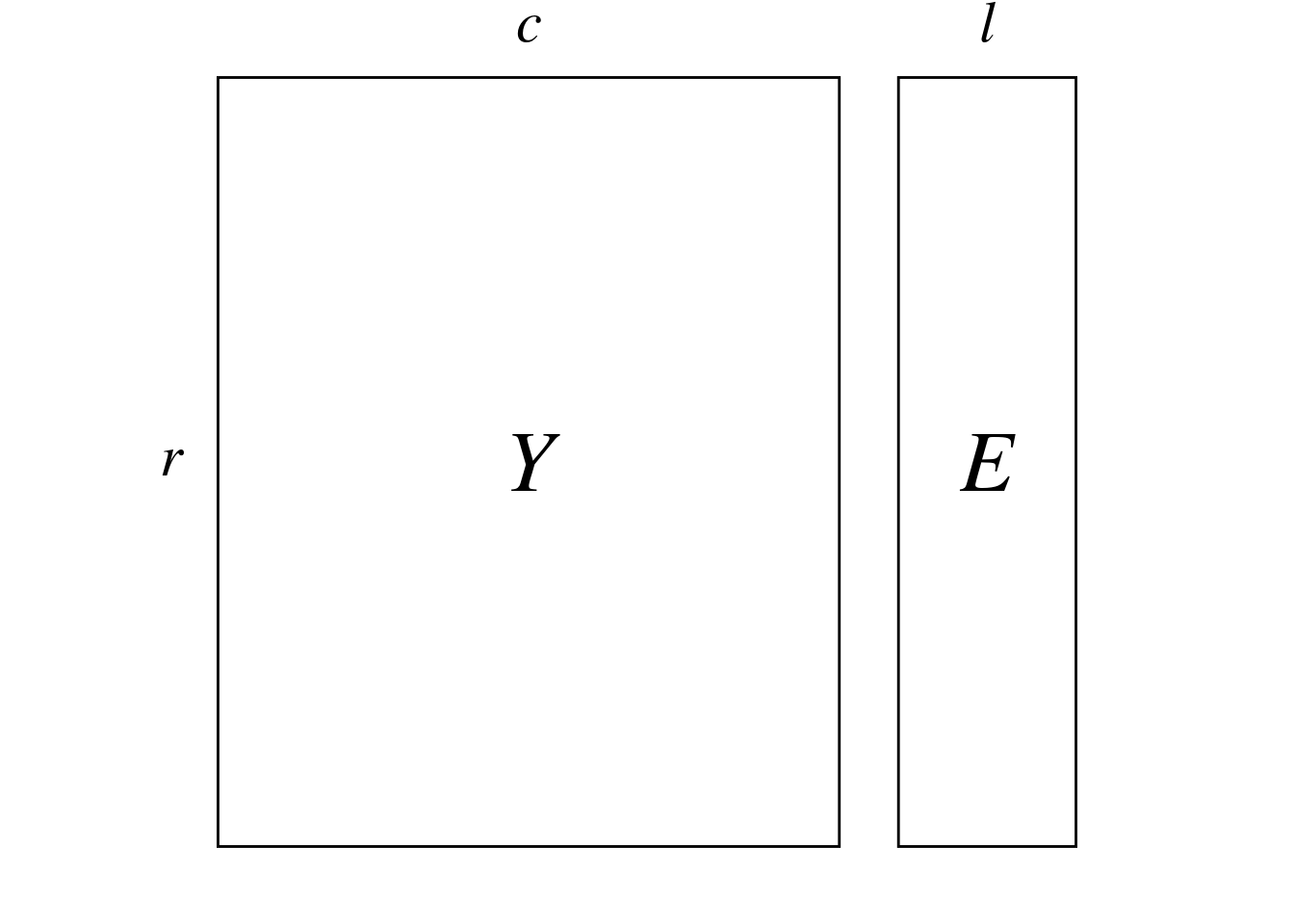
Here, \(Y\) represents the abundance of different bird species (columns) at different sites (rows):

Code

knitr::kable(head(Y))

sp1	sp3	sp4	sp6	sp8	sp9	sp10	sp11	sp12	sp13	sp15	sp16	sp17	sp18	sp19	sp22
1	1	1	1	2	0	1	1	0	0	0	0	0	0	1	0
2	0	2	1	5	0	2	0	2	4	3	3	0	3	1	2
5	0	2	1	2	0	1	2	0	0	0	0	0	3	2	1
3	0	0	1	4	1	0	1	0	0	0	0	0	2	0	1
5	0	1	1	2	0	0	3	0	0	0	1	0	3	1	1
1	0	1	2	3	1	2	1	0	0	1	0	1	2	2	3

\(E\) represents environmental variables (columns) associated to each site (rows).

Code

knitr::kable(head(E))

elevation	patch_area	perc_forests	perc_grasslands	ShannonLandscapeDiv
10	6.28	7.7882	67.7785	0.232
30	7.92	16.4129	43.4066	0.274
430	83.24	24.4526	28.4995	0.274
420	140.83	41.9966	34.2412	0.260
400	140.83	41.9966	34.2412	0.260
500	0.50	7.5445	67.0780	0.240

(r <- dim(Y)[1])

[1] 26

(c <- dim(Y)[2])

[1] 21

(l <- dim(E)[2])

[1] 6

Computation

TL;DR

We have a data matrix \(Y\) (\(r \times c\)) and a matrix \(E\) (\(r \times l\)) of predictors variables.

We regress \(P_0\) (“centered” \(Y\)) on \(E_{stand}\) (which is the centered and scaled \(E\) matrix):

\[ \hat{P_0} = D_r^{1/2} E_{stand}B \]

Then, we diagonalize matrix \(S_{\hat{P_0}^\top \hat{P_0}} = \hat{P_0}^\top\hat{P_0}\).

\[ S_{\hat{P_0}^\top\hat{P_0}} = V_0 \Lambda V_0^{-1} \]

The matrix \(V_0\) (\(c \times \text{mindim}\)) contains the loadings of the columns (species) of the contingency table. There are \(\text{mindim} = \min(r-1, c, l)\) non-null eigenvalues.

Then, we can find the rows (sites) observed scores \(U_0\) (\(r \times \text{mindim}\)) from the eigenvectors of the multivariate space using the following formula:

\[ U_0 = P_0 V_0 \Lambda^{-1/2} \]

Here, it is important to note that \(U_0\) contains the loadings of the sites computed from the observed data matrix \(P_0\), i.e. the latent ordination of the sites not taking into account the sites variables. The position of the sites taking into account the regression will be defined below in the scalings section.

Finally, we define the following transformations of \(U_0\) and \(V_0\) (\(V_0\) corresponds to c1):

\[ \left\{ \begin{array}{ll} U &= D_r^{-1/2} U_0\\ V &= D_c^{-1/2} V_0\\ \end{array} \right. \] This transformation is similar to the transformation applied to CA eigenvectors.

Transform matrix

We start by “centering” the matrix \(Y\) to get \(P_0\) (just like with CA).

\[ P = Y/y_{\cdot \cdot} \]

\[ P_0 = [p_{0ij}] = \left[ \frac{p_{ij} - p_{i\cdot} p_{\cdot j}}{\sqrt{p_{i\cdot} p_{\cdot j}}} \right] \]

Here, we have:

Code

P <- Y/sum(Y)

# Initialize P0 matrix
P0 <- matrix(ncol = ncol(Y), nrow = nrow(Y))
colnames(P0) <- colnames(Y)
rownames(P0) <- rownames(Y)

for(i in 1:nrow(Y)) { # For each row
  for (j in 1:ncol(Y)) { # For each column
    # Do the sum
    pi_ <- sum(P[i, ])
    p_j <- sum(P[, j])
    
    # Compute the transformation
    P0[i, j] <- (P[i, j] - (pi_*p_j))/sqrt(pi_*p_j)
  }
}

Code

knitr::kable(head(P0))

sp1	sp2	sp3	sp4	sp5	sp6	sp7	sp8	sp9	sp10	sp11	sp12	sp13	sp14	sp15	sp16	sp17	sp18	sp19	sp21	sp22
-0.0246174	-0.0235678	0.1819102	0.0177849	-0.0086058	0.0190444	-0.0060852	0.0389306	-0.0172115	0.0177849	0.0142185	-0.0285421	-0.0121704	-0.0086058	-0.0172115	-0.0136069	-0.0172115	-0.0425963	0.0259875	-0.0227687	-0.0250899
-0.0700532	-0.0430288	-0.0192431	-0.0075494	-0.0157119	-0.0362309	-0.0111100	0.0317935	-0.0314238	-0.0075494	-0.0702658	0.0257394	0.3429284	-0.0157119	0.1622254	0.2201063	-0.0314238	0.0004761	-0.0290665	-0.0415698	0.0427538
0.0325898	-0.0342433	-0.0153141	0.0216502	-0.0125039	-0.0148135	-0.0088416	-0.0092517	-0.0250078	-0.0160655	0.0166286	-0.0414707	-0.0176832	-0.0125039	-0.0250078	-0.0197704	-0.0250078	0.0364300	0.0331807	-0.0330822	0.0191867
0.0149125	-0.0283250	-0.0126673	-0.0444862	-0.0103428	0.0023441	-0.0073135	0.0865729	0.0773724	-0.0444862	-0.0024017	-0.0343033	-0.0146270	-0.0103428	-0.0206857	-0.0163535	-0.0206857	0.0280484	-0.0407198	-0.0273646	0.0371130
0.0381182	-0.0333300	-0.0149056	-0.0135976	-0.0121704	-0.0123509	-0.0086058	-0.0058019	-0.0243408	-0.0523468	0.0573758	-0.0403646	-0.0172115	-0.0121704	-0.0243408	0.0861662	-0.0243408	0.0407749	-0.0055815	-0.0321998	0.0216837
-0.0648859	-0.0351329	-0.0157119	-0.0184176	-0.0128287	0.0201080	-0.0090713	0.0163368	0.0533995	0.0183431	-0.0220164	-0.0425480	-0.0181425	-0.0128287	0.0533995	-0.0202840	0.0533995	0.0003888	0.0298152	-0.0339416	0.1252960

Weights on \(E\)

We standardize \(E\) as \(E_{stand}\), but we standardize so that the variables associated to the sites which have more observations have more weight. Therefore, we standardize \(E\) with the weights \(y_{i\cdot}/r\).

E_wt <- rowSums(Y)/nrow(E)

Estand <- scalewt(E, wt = E_wt)

Code

knitr::kable(head(Estand))

location	elevation	patch_area	perc_forests	perc_grasslands	ShannonLandscapeDiv
-0.8940191	-1.4578384	-0.5429520	-1.0404731	1.0369741	-1.0351817
-0.8940191	-1.3502706	-0.5081483	-0.3311255	-0.4345644	1.0954816
-0.8940191	0.8010856	1.0902771	0.3301082	-1.3346326	1.0954816
-0.8940191	0.7473017	2.3124400	1.7730331	-0.9879574	0.3852605
-0.8940191	0.6397339	2.3124400	1.7730331	-0.9879574	0.3852605
-0.8940191	1.1775730	-0.6656140	-1.0605165	0.9946790	-0.6293411

Conceptually, it is equivalent to using the inflated matrix \(E_{infl}\) to compute its mean \(\bar{E}_{infl}\) and standard deviation \(\sigma(E_{infl})\) per column. In \(E_{infl}\), the rows corresponding to each site are duplicates as many times as there are observations for this given site (so that \(E_{infl}\) is of dimension \(y_{\cdot \cdot} \times l\)).

\[ E_{stand} = \frac{E - \bar{E}_{infl}}{\sigma(E_{infl})} \]

With our data: first, we compute \(E_{infl}\):

Code

Einfl <- matrix(data = 0,
                ncol = ncol(E), 
                nrow = sum(Y))
colnames(Einfl) <- colnames(E)
rownames(Einfl) <- 1:nrow(Einfl)

# Get the number of times to duplicate each site
nrep_sites <- rowSums(Y)

nrstart <- 0
for (i in 1:nrow(E)) {
  ri <- as.matrix(E)[i, ]
  
  rname <- rownames(E)[i]
  
  # Get how many times to duplicate this site
  nr <- nrep_sites[as.character(rname)]
  
  Einfl[(nrstart+1):(nrstart+nr), ] <- matrix(rep(ri, nr), 
                                              nrow = nr, 
                                              byrow = TRUE)
  
  rownames(Einfl)[(nrstart+1):(nrstart+nr)] <- paste(rname,
                                                     1:nr,
                                                     sep = "_")
  nrstart <- nrstart + nr
}

paste("Dimension of Einfl:", paste(dim(Einfl), collapse = " "))

[1] "Dimension of Einfl: 493 6"

Then, we compute the mean and standard deviation per column and standardize \(E\).

Code

Einfl_mean <- apply(Einfl, 2, mean)

n <- nrow(Einfl)
Einfl_sd <- apply(Einfl, 2, 
                  function(x) sd(x)*sqrt((n-1)/n))

Code

Estand2 <- scale(E, 
                 center = Einfl_mean,
                 scale = Einfl_sd)

all(abs(Estand2/Estand - 1) < zero)

[1] TRUE

Regression

After that, we perform the weighted multiple linear regression of \(P_0\) by \(E_{stand}\). \(P_0\) is approximated by \(\hat{P_0}\) using multiple linear regression on \(E_{stand}\): for each row, we can write \(\hat{p_{0i\cdot}} = b_0 + b_1 e_{1\cdot} + \ldots + b_e e_{l\cdot}\), where \(e_i\) are columns of \(E_{stand}\) and \(b_i\) are regression coefficients.

In a matrix form, it is written:

\[ \hat{P_0} = D_r^{1/2}E_{stand}B \]

Where

\[ B = [E_{stand}^\top D_r E_{stand}]^{-1}E_{stand}^\top D_r^{1/2}P_0 \]

With our example:

# Diagonal matrix weights
dr <- rowSums(P)
Dr <- diag(dr)
colnames(Dr) <- rownames(P)

# Regression coefficient
B <- solve(t(Estand) %*% Dr %*% Estand) %*% t(Estand) %*% diag(dr^(1/2)) %*% P0

# Compute predicted values
P0hat <- diag(dr^(1/2)) %*% Estand %*% B
colnames(P0hat) <- colnames(P0)
rownames(P0hat) <- rownames(P0)

Now, we can get the predicted values for \(P_0\). For instance, let’s plot predicted vs observed values for site 2:

# Get predicted and observed values for one site
ind <- 2

pred <- P0hat[ind, ]
obs <- P0[ind, ]

Code

df <- data.frame(predicted = pred, 
                 observed = obs, 
                 names = names(pred))
df<- df |> 
  tidyr::pivot_longer(cols = c("predicted", "observed"),
                      names_to = "type")

ggplot(df, aes(x = reorder(names, value, decreasing = TRUE), 
               y = value, col = type, group = type)) +
  geom_point() +
  geom_line() +
  theme_linedraw() +
  ylab("Values of P0") +
  xlab("Species") +
  theme(axis.text.x = element_text(angle = 90, hjust = 1))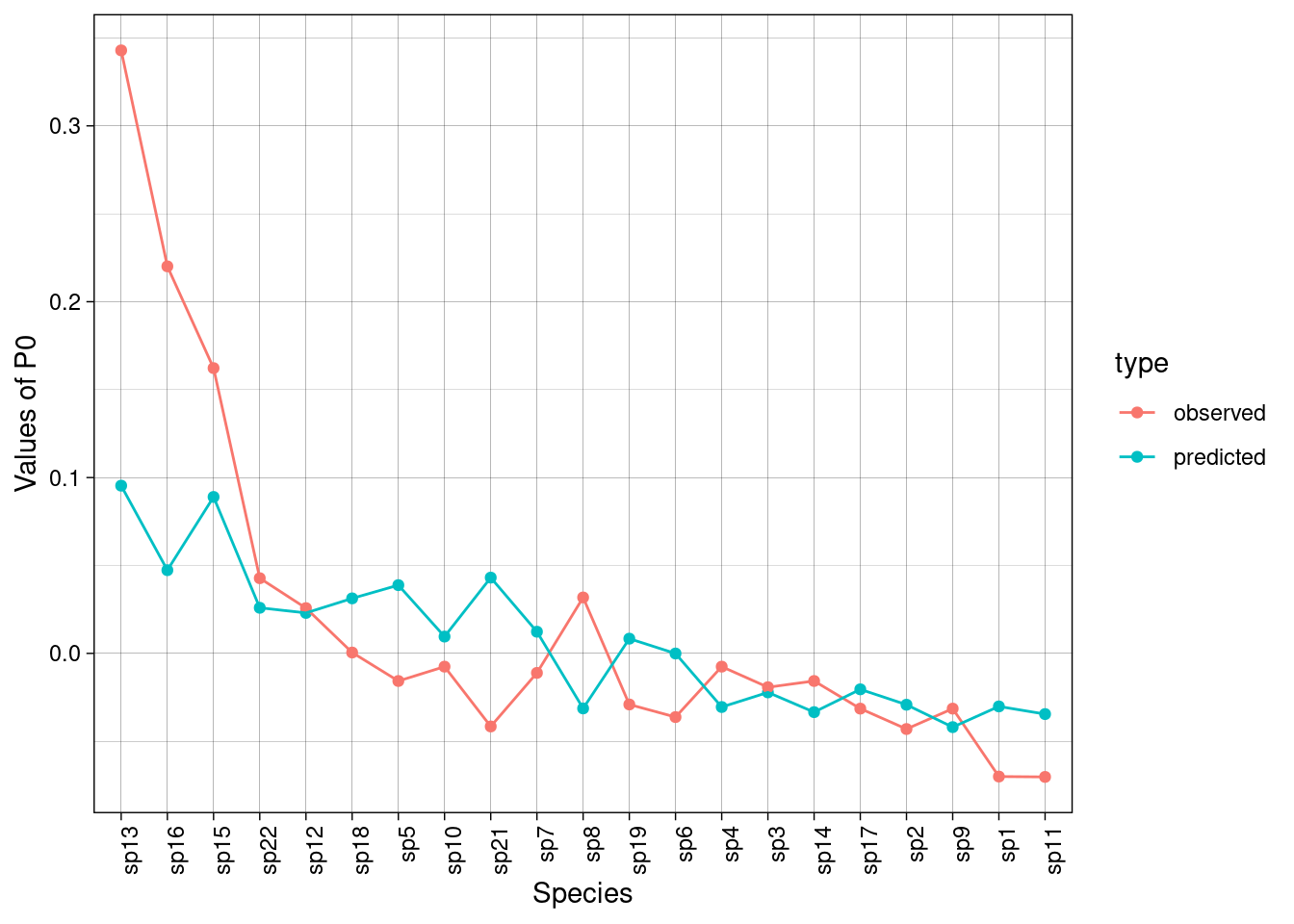

Diagonalization of \(S_{\hat{P_0}^\top \hat{P_0}}\)

Then, we diagonalize the covariance matrix of predicted values \(S_{\hat{P_0}^\top \hat{P_0}}\).

First, we compute the covariance matrix (note that here we don’t divide by the degrees of freedom).

\[ S_{\hat{P_0}^\top \hat{P_0}} = \hat{P_0}^\top \hat{P_0} \]

Spp <- t(P0hat) %*% P0hat

Code

# Covariance matrix of predicted P0 is equal to that
Spe <- t(P0hat) %*% diag(dr^(1/2)) %*% as.matrix(Estand)
See <- t(Estand) %*% Dr %*% as.matrix(Estand)
Spp2 <- Spe %*% solve(See) %*% t(Spe)

all(abs(Spp/Spp2 - 1) < zero)

[1] TRUE

We diagonalize \(S_{\hat{P_0}^\top \hat{P_0}}\):

\[ S_{\hat{P_0}^\top \hat{P_0}} = V_0 \Lambda V_0^{-1} \]

\(\Lambda\) is the matrix of eigenvalues (there are \(\min(r-1, c, l)\) non-null eigenvalues) and \(V_0\) contains the columns (species) loadings.

neig <- min(c(r-1, c, l))

Here, \(r-1 =\) 25, \(c =\) 21 and \(l =\) 6 so the minimum (and the number of eigenvalues) is 6.

eig <- eigen(Spp)

(lambda <- eig$values) # There are l = 6 non-null eigenvalues

 [1]  1.846574e-01  1.571586e-01  1.009501e-01  8.711508e-02  3.222443e-02
 [6]  1.476469e-02  9.276798e-18  8.416776e-18  2.476628e-18  1.422189e-18
[11] -1.212603e-18 -1.597223e-18 -1.677170e-18 -2.007096e-18 -3.488219e-18
[16] -3.614024e-18 -5.174948e-18 -5.675276e-18 -6.196745e-18 -6.258539e-18
[21] -7.334976e-18

lambda <- lambda[1:neig]

Lambda <- diag(lambda)
V0 <- eig$vectors[, 1:neig] # We keep only the eigenvectors
rownames(V0) <- colnames(Y)

Finally, we can get the ordination of rows (sites) by projecting the observed values (matrix \(P_0\)) onto the axes defined by the diagonalization (\(V_0\)):

\[ U_0 = P_0 V_0 \Lambda^{-1/2} \]

U0 <- P0 %*% V0 %*% diag(lambda^(-1/2))
rownames(U0) <- rownames(U0)

apply(U0, 2, varfacwt, wt = rowSums(P)) # Norm?

[1] 0.06513814 0.06770504 0.08019396 0.07772885 0.12867946 0.10202597

Note

The rows loadings \(U_0\) are different from the loadings obtained by diagonalizing \(S_{hat{P_0} \hat{P_0}^\top}\) or performing the SVD of \(\hat{P_0}\), because \(U_0\) does not contain the loadings of \(\hat{P_0}\) but the loadings of \(P_0\).

# This is not the same as diagonalizing S_ppt
Sppt <- P0hat %*% t(P0hat)
eig2 <- eigen(Sppt)

all(abs(eig2$vectors[,1:neig]/U0 - 1) < zero) # Eigenvectors are different

[1] FALSE

# We perform the SVD
sv <- svd(P0hat)

all(abs(abs(sv$u[, 1:neig]/U0) - 1) < zero) # Eigenvectors are different for U0

[1] FALSE

all(abs(abs(sv$v[, 1:neig]/V0) - 1) < zero) # But they are the same for V0

[1] TRUE

# If U was computed as below (using the matrix of predicted values), it would give the same results as the diagonalization/SVD above (but it is not the case).

# Compute rows loadings differently
Uhat <- P0hat %*% V0 %*% diag(lambda^(-1/2))

all(abs(abs(Uhat/eig2$vectors[,1:neig]) - 1) < zero) # Eigenvectors are the same

[1] TRUE

all(abs(abs(sv$u[, 1:l]/eig2$vectors[,1:l]) - 1) < zero) # Eigenvectors are the same

[1] TRUE

Compute \(U\) and \(V\)

We compute \(U\) and \(V\) as:

\[ \left\{ \begin{array}{ll} U &= D_r^{-1/2} U_0\\ V &= D_c^{-1/2} V_0\\ \end{array} \right. \]

First, we define the diagonal matrices with rows and columns weights (respectively \(D_r\) and \(D_c\)).

# Define weights vectors and matrices
dr <- rowSums(P)
dc <- colSums(P)

Dr <- diag(dr)
Dc <- diag(dc)

# Sites
U <- diag(dr^(-1/2)) %*% U0
  
# Species
V <- diag(dc^(-1/2)) %*% V0

apply(U, 2, varfacwt, wt = dr)/lambda # variance larger than lambda, because it contains the residuals of P0hat as well!!

[1]   7.244385   9.261437  14.814747  19.935957  96.297789 180.619015

apply(V, 2, varfacwt, wt = dc) # variance is one

[1] 1 1 1 1 1 1

Scaling

TL;DR

As with CA, we have scalings type 1, 2 and 3. There are 2 differences with CA:

For the sites, we have 3 types of scores: the predicted sites scores \(Z\) (LC scores), computed from the regression, the “observed” sites scores \(U\) computed from the observed data matrix, and the weighted averages \(U^\star\) (WA scores), computed from the species scores.
There are also scalings for the correlations of the explanatory variables with the axes.

Scaling type 1 (\(\alpha = 1\))

WA scores for rows (sites): \(U^\star = U \Lambda^{1/2}\) (ls)
LC scores for rows (sites): \(Z_1 = D_r^{-1/2} \hat{P_0} V_0\) (li)
Columns (species) scores: \(V = D_c^{-1/2} V_0\) (c1)
Variables scores: \(BS_1 = E_{stand}^\top D_r Z_{stand} \Lambda^{1/2}\)

Scaling type 2 (\(\alpha = 0\))

WA scores for rows (sites): \(U = D_r^{-1/2} U_0\) (not computed by ade4: sort of ls1, but variance not normed to one)
LC scores for rows (sites): \(Z_2 = D_r^{-1/2}\hat{P_0} V_0 \Lambda^{-1/2}\) (l1)
Columns (species) scores: \(V^\star = V \Lambda^{1/2}\) (co)
Variables scores: \(BS_2 = E_{stand}^\top D_r Z_{stand}\)

Scaling type 3 (\(\alpha = 1/2\))

WA scores for rows (sites): \(\hat{S}_3 = U \Lambda^{1/4}\)
LC scores for rows (sites): \(Z_3 = D_r^{-1/2}\hat{P_0} V_0 \Lambda^{-1/4}\)
Columns (species) scores: \(S_3 = V \Lambda^{1/4}\)
Variables scores: \(BS_3 = E_{stand}' D_r Z_{stand}\Lambda^{1/4}\)

\(V^\star\) (columns/species) and \(U^\star\) (rows/sites) correspond to weighted averagings, and cab be computed from \(U\) (rows/sites) (resp. \(V\) (columns/species)). See Equation 1 and Equation 2 below.

How to find the fa (i.e. correlation coefficients for each environmental variable in the multivariate space)??

Let’s compute CCA with ade4 to compare results.

ca <- dudi.coa(Y, 
               nf = c-1, 
               scannf = FALSE)
cca <- pcaiv(dudi = ca, 
             df = E,
             scannf = FALSE,
             nf = neig)

lambda[1:neig]/cca$eig # Eigenvalues are the same as computed manually

[1] 1 1 1 1 1 1

Pre-computations

The scores for the explanatory variables are computed from matrix \(Z_{stand}\): so we first need to standardize \(Z\) into \(Z_{stand}\) (the computation can involve \(Z_1\), \(Z_2\) or \(Z_3\) (defined below) and give the same result).

\(Z_1\), \(Z_2\) or \(Z_3\) are defined as some variation of:

\[Z_i = D_r^{-1/2} \hat{P}_0 V_0 \Lambda^\alpha\] where \(\alpha\) is an exponent equal to 0, -1/2 or -1/4. This equation corresponds to the projection of the predicted data matrix \(\hat{P}_0\) onto the multivariate space.

# Compute Z1
Z1 <- diag(dr^(-1/2)) %*% P0hat %*% V0

apply(Z1, 2, varfacwt)

[1] 0.17463933 0.17429419 0.09984546 0.08291203 0.03437735 0.01521229

Z_wt <- E_wt
Zstand <- scalewt(Z1, wt = Z_wt)

It is the same as computing with the inflated matrix (below):

Code

# Compute inflated matrix ------
Zinfl <- matrix(data = 0,
                ncol = ncol(Z1), 
                nrow = sum(Y))
rownames(Zinfl) <- 1:nrow(Zinfl)
# Give names to Z1
rownames(Z1) <- rownames(Y)

# Get the number of times to duplicate each site
nrep_sites <- rowSums(Y)

nrstart <- 0
for (i in 1:nrow(Z1)) {
  ri <- Z1[i, ]
  
  rname <- rownames(Z1)[i]
  
  # Get how many times to duplicate this site
  nr <- nrep_sites[as.character(rname)]
  
  Zinfl[(nrstart+1):(nrstart+nr), ] <- matrix(rep(ri, nr), 
                                              nrow = nr, 
                                              byrow = TRUE)
  
  rownames(Zinfl)[(nrstart+1):(nrstart+nr)] <- paste(rname, 
                                                     1:nr, 
                                                     sep = "_")
  nrstart <- nrstart + nr
}

# Compute mean/sd ------
Zinfl_mean <- apply(Zinfl, 2, mean)

n <- nrow(Zinfl)
Zinfl_sd <- apply(Zinfl, 2, 
                  function(x) sd(x)*sqrt((n-1)/n))

# Compute Zstand ------
Zstand2 <- scale(Z1, 
                 center = Zinfl_mean,
                 scale = Zinfl_sd)

all(abs(Zstand2/Zstand - 1) < zero)

[1] TRUE

Scaling type 1

Here, \(\chi^2\) distances between rows (sites) are preserved they are positioned at the centroid of species.

the rows (sites) scores can be positioned by averaging: \(U^\star = U \Lambda^{1/2}\) (ls) or by predicted positions \(Z_1 = D_r^{-1/2} \hat{P_0} V_0\) (li)
the columns (species) scores are positioned at variance 1 \(V = D_c^{-1/2} V_0\) (c1)
the explanatory variable score are \(BS_1 = E_{stand}^\top D_r Z_{stand}\Lambda^{1/2}\)

# Rows WA scores
Ustar <- U %*% diag(lambda^(1/2))

# Variables correlation
BS1 <- t(Estand) %*% Dr %*% Zstand %*% sqrt(Lambda)

If we compare to the results obtained with ade4, we can see what each score corresponds to.

all(abs(abs(Z1/cca$li) - 1) < zero) # Predicted sites scores

[1] TRUE

all(abs(abs(Ustar/cca$ls) - 1) < zero) # Averaging sites scores

[1] TRUE

all(abs(abs(V/cca$c1) - 1) < zero) # Variance 1 species scores

[1] TRUE

# What does the BS1 correspond to?
res <- as.matrix(cca$cor)/(BS1 %*% diag(lambda^(-1/2)) )
all(abs(abs(res) - 1) < zero)

[1] TRUE

We know that \(V\)/c1 is of variance 1 (computed above). Below we show that \(Z_1\)/li is of variance \(\lambda\) and try to get the variance of \(U^\star\)/ls.

# The CCA weights can be recovered from data (modulo a constant)
cca$lw/E_wt

         1          2          3          4          5          6          7 
0.05273834 0.05273834 0.05273834 0.05273834 0.05273834 0.05273834 0.05273834 
         8          9         10         11         12         13         14 
0.05273834 0.05273834 0.05273834 0.05273834 0.05273834 0.05273834 0.05273834 
        15         16         17         18         19         20         21 
0.05273834 0.05273834 0.05273834 0.05273834 0.05273834 0.05273834 0.05273834 
        22         23         24         25         26 
0.05273834 0.05273834 0.05273834 0.05273834 0.05273834

cca$cw/(colSums(Y)/ncol(Y))

       sp1        sp2        sp3        sp4        sp5        sp6        sp7 
0.04259635 0.04259635 0.04259635 0.04259635 0.04259635 0.04259635 0.04259635 
       sp8        sp9       sp10       sp11       sp12       sp13       sp14 
0.04259635 0.04259635 0.04259635 0.04259635 0.04259635 0.04259635 0.04259635 
      sp15       sp16       sp17       sp18       sp19       sp21       sp22 
0.04259635 0.04259635 0.04259635 0.04259635 0.04259635 0.04259635 0.04259635

apply(Z1, 2, varwt, wt = cca$lw)/cca$eig # Z1 variance = eigenvalues

[1] 1 1 1 1 1 1

apply(Ustar, 2, varwt, wt = cca$lw)

[1] 0.24702157 0.22874662 0.15097579 0.15129471 0.09999697 0.03937424

Weighted averaging

Similarly to the CA case, \(U^\star\) (sites coordinates) can be obtained from species coordinates, weighted by the observed data matrix:

\[ U^\star = \left\{ \begin{array}{ll} D_r^{-1/2} P_0 V_0 \qquad &\text{(from } V_0 \text{)}\\ D_r^{-1/2} P_0 D_c^{1/2} V \qquad &\text{(from } V \text{)}\\ D_r^{-1} P V \qquad &\text{(from } V \text{ and } P \text{)}\\ \end{array} \right. \tag{1}\]

# With V0
Ustar_wa <- diag(dr^(-1/2)) %*% P0 %*% V0
res <- Ustar_wa/Ustar
all(res[, 1:neig] - 1 < zero)

[1] TRUE

# With V
Ustar_wa_V <- diag(dr^(-1/2)) %*% P0 %*% diag(dc^(1/2)) %*% V
res <- Ustar_wa_V/Ustar
all(res[, 1:neig] - 1 < zero)

[1] TRUE

# With V and P
Ustar_wa_legendre <- diag(dr^(-1)) %*% P %*% V
res <- Ustar_wa_legendre/Ustar
all(res[, 1:neig] - 1 < zero)

[1] TRUE

Plots

In these plots, we use \(V\)/c1 for species coordinates.

For sites, we can plot the predicted scores for sites (LC scores = \(Z_1\)/li):

Code

mult <- 10

# LC scores
multiplot(indiv_row = Z1, indiv_col = V, 
          indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y), 
          var_row = BS1, var_row_lab = colnames(E),
          row_color = params$colsite, col_color = params$colspp,
          mult = mult,
          eig = lambda) +
  ggtitle("LC scores for sites and species\nnormed at 1")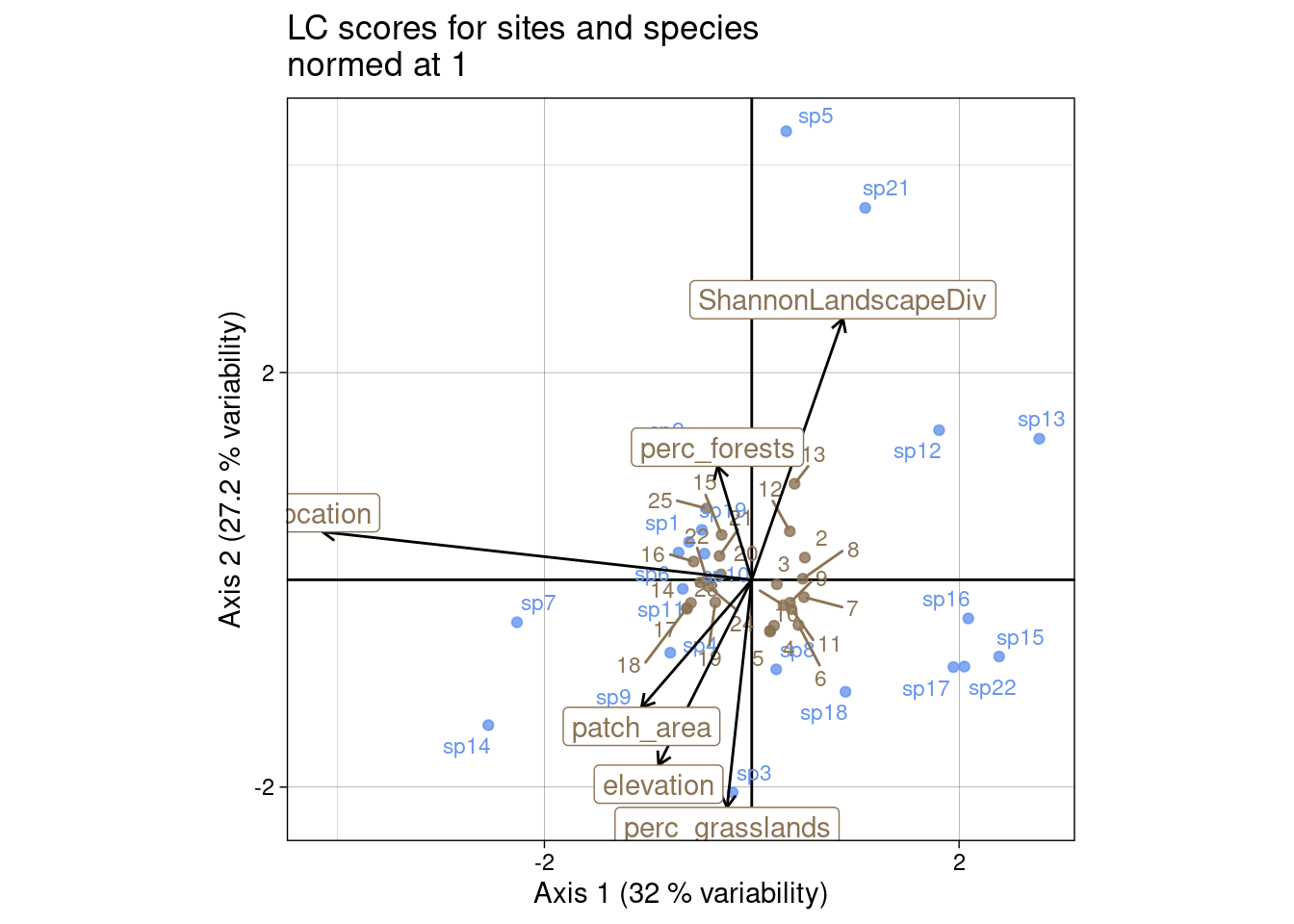

Code

s.label(cca$c1, # Species constrained at variance 1
        plabels.optim = TRUE,
        plabels.col  = params$colspp,
        ppoints.col = params$colspp,
        main = "LC scores for sites and species\nnormed at 1")
s.label(cca$li, # Predicted sites scores
        plabels.optim = TRUE,
        plabels.col  = params$colsite,
        ppoints.col = params$colsite,
        add = TRUE)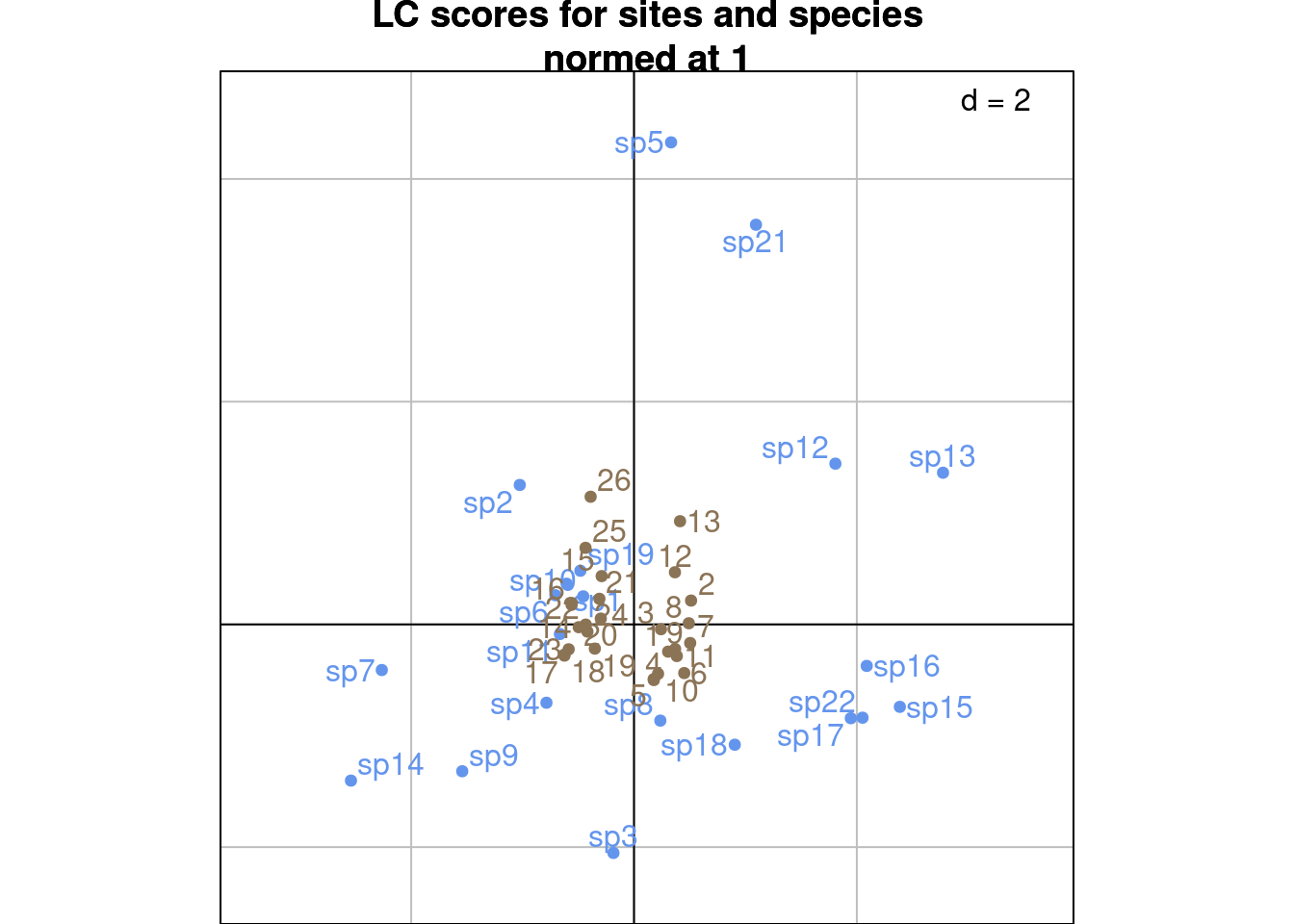

We can also plot the WA scores for sites (\(U^\star\)/ls):

Code

# WA scores
multiplot(indiv_row = Ustar, indiv_col = V, 
          indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y), 
          var_row = BS1, var_row_lab = colnames(E),
          row_color = params$colsite, col_color = params$colspp,
          mult = mult,
          eig = lambda) +
  ggtitle("WA scores for sites and species\nnormed at 1")

Code

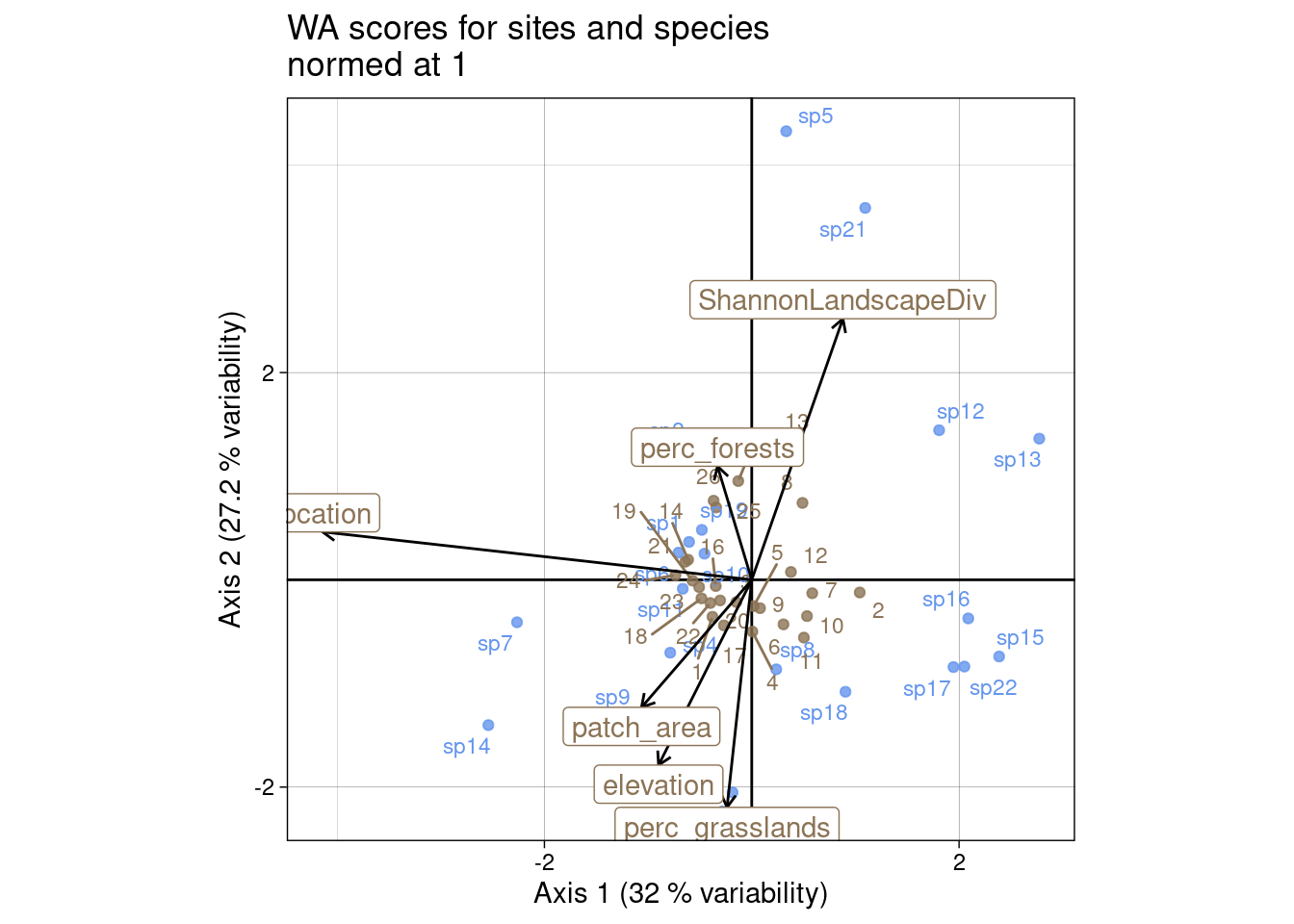
s.label(cca$c1, # Species constrained at variance 1
        plabels.optim = TRUE,
        plabels.col  = params$colspp,
        ppoints.col = params$colspp,
        main = "WA scores for sites and species\nnormed at 1")
s.label(cca$ls, # WA sites scores
        plabels.optim = TRUE,
        plabels.col  = params$colsite,
        ppoints.col = params$colsite,
        add = TRUE)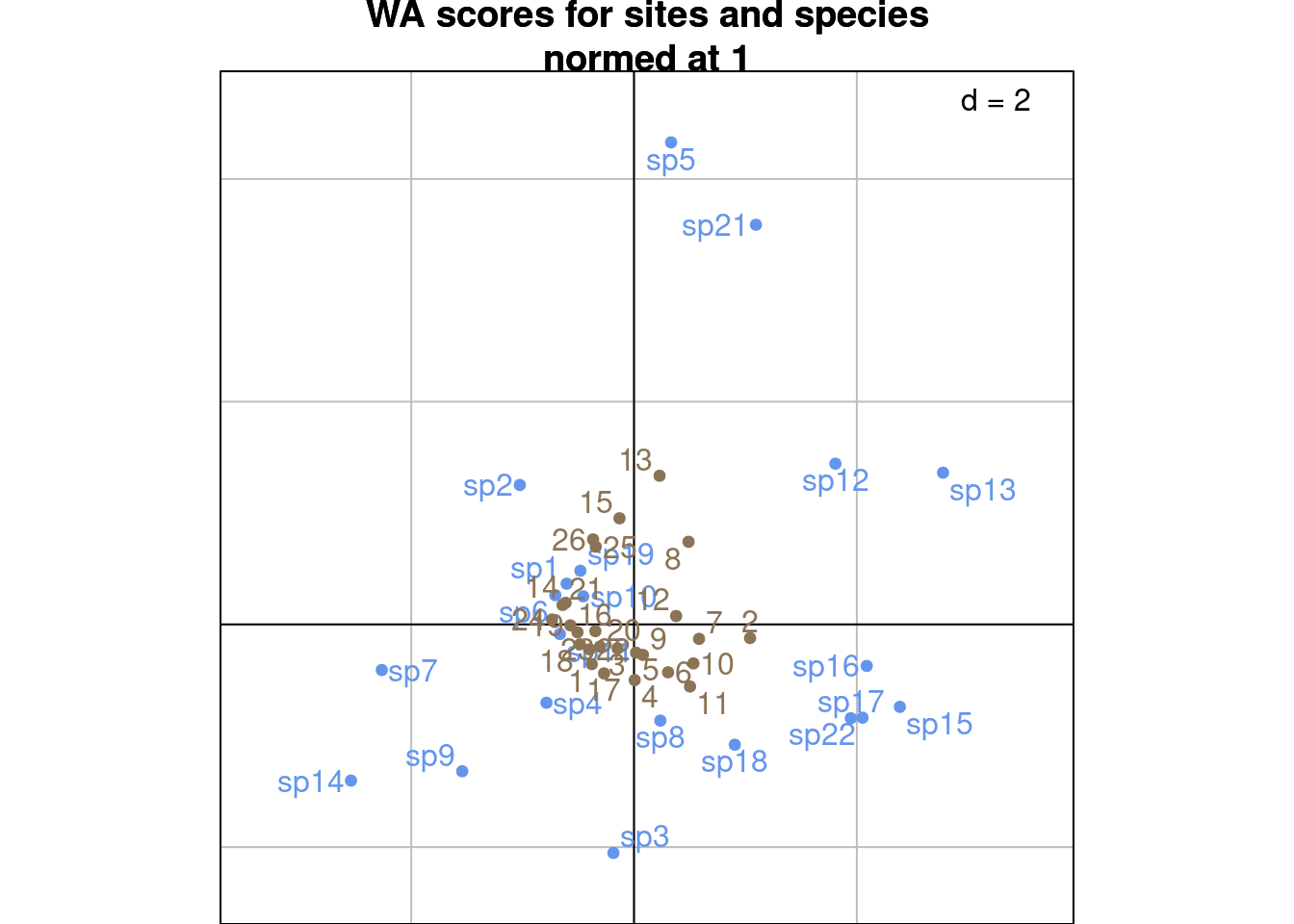

Scaling type 2

Here, \(\chi^2\) distances between columns (species) are preserved they are positioned at the centroid of sites.

the rows (sites) scores can be \(U = D_r^{-1/2} U_0\) (variance 1) or \(Z_2 = D_r^{-1/2} \hat{P_0} V_0 \Lambda^{-1/2}\) (l1) (predicted sites scores)
the columns (species) scores are \(V^\star = V \Lambda^{1/2}\) (co) (WA scores from sites latent ordination)
the explanatory variable score are \(BS_2 = E_{stand}^\top D_r Z_{stand}\)

# Row predicted scores
Z2 <- diag(dr^(-1/2)) %*% P0hat %*% V0 %*% diag(lambda^(-1/2))

# Columns WA scores
Vstar <- V %*% Lambda^(1/2)

# Variables correlation
BS2 <- t(Estand) %*% Dr %*% Zstand

If we compare to the results obtained with ade4, we can see what each score corresponds to.

all(abs(abs(Z2/cca$l1) - 1) < zero) # Predicted sites scores of variance 1

[1] TRUE

# U is not computed by ade4 so we compute it from ls (corresponding to Ustar)
ls1_ade4 <- as.matrix(cca$ls) %*% diag(lambda^(-1/2))
all(abs(abs(ls1_ade4/U) - 1) < zero)

[1] TRUE

all(abs(abs(Vstar/cca$co) - 1) < zero) # Averaging column scores

[1] TRUE

all(abs(abs(cca$cor/BS2) - 1) < zero) # Variables correlations

[1] TRUE

Below we show that \(V^\star\)/co is of variance \(\lambda\), \(Z_2\)/l1 is of variance 1 and try to get the variance of \(U\)/ls1.

apply(Vstar, 2, varwt, wt = cca$cw)/cca$eig # Vstar variance = eigenvalues

[1] 1 1 1 1 1 1

apply(Z2, 2, varwt, wt = cca$lw) # Z variance = 1

[1] 1 1 1 1 1 1

apply(ls1_ade4, 2, varwt, wt = cca$lw) # ?

[1] 1.337729 1.455514 1.495549 1.736722 3.103141 2.666784

Weighted averaging

\(V^\star\) (species coordinates) can be obtained from sites coordinates, weighted by the predicted data matrix. Contrary to the CA case, sites coordinates are not weighted by \(P_0\) (observed) but by \(\hat{P}_0\) (predicted):

\[ V^\star = \left\{ \begin{array}{ll} D_c^{-1/2} \hat{P}_0^\top U_0 \qquad &\text{(from } U_0 \text{)}\\ D_c^{-1/2} \hat{P}_0^\top D_r^{1/2} U \qquad &\text{(from } U \text{)} \end{array} \right. \tag{2}\]

# U0
Vstar_wa <- diag(dc^(-1/2)) %*% t(P0hat) %*% U0
res <- Vstar_wa/Vstar
all(res[, 1:neig] - 1 < zero)

[1] TRUE

# U
Vstar_wa_U <- diag(dc^(-1/2)) %*% t(P0hat) %*% diag(dr^(1/2)) %*% U
res <- Vstar_wa_U/Vstar
all(res[, 1:neig] - 1 < zero)

[1] TRUE

# Tests with score Z2
Vstar_wa_Z <- diag(dc^(-1)) %*% t(P) %*% Z2
res <- Vstar_wa_Z/Vstar
all(res[, 1:neig] - 1 < zero)

[1] TRUE

Plots

In these plots, we always use WA scores (\(V^\star\)/co) for the columns.

We can plot the columns WA scores (\(V^\star\)/co) with the predicted scores for sites (LC scores) (\(Z_2\)/l1):

Code

mult <- 1

# LC scores
multiplot(indiv_row = Z2, indiv_col = Vstar, 
          indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y), 
          var_row = BS2, var_row_lab = colnames(E),
          row_color = params$colsite, col_color = params$colspp,
          mult = mult,
          eig = lambda) +
  ggtitle("Specis WA scores with\nsites LC scores of variance 1")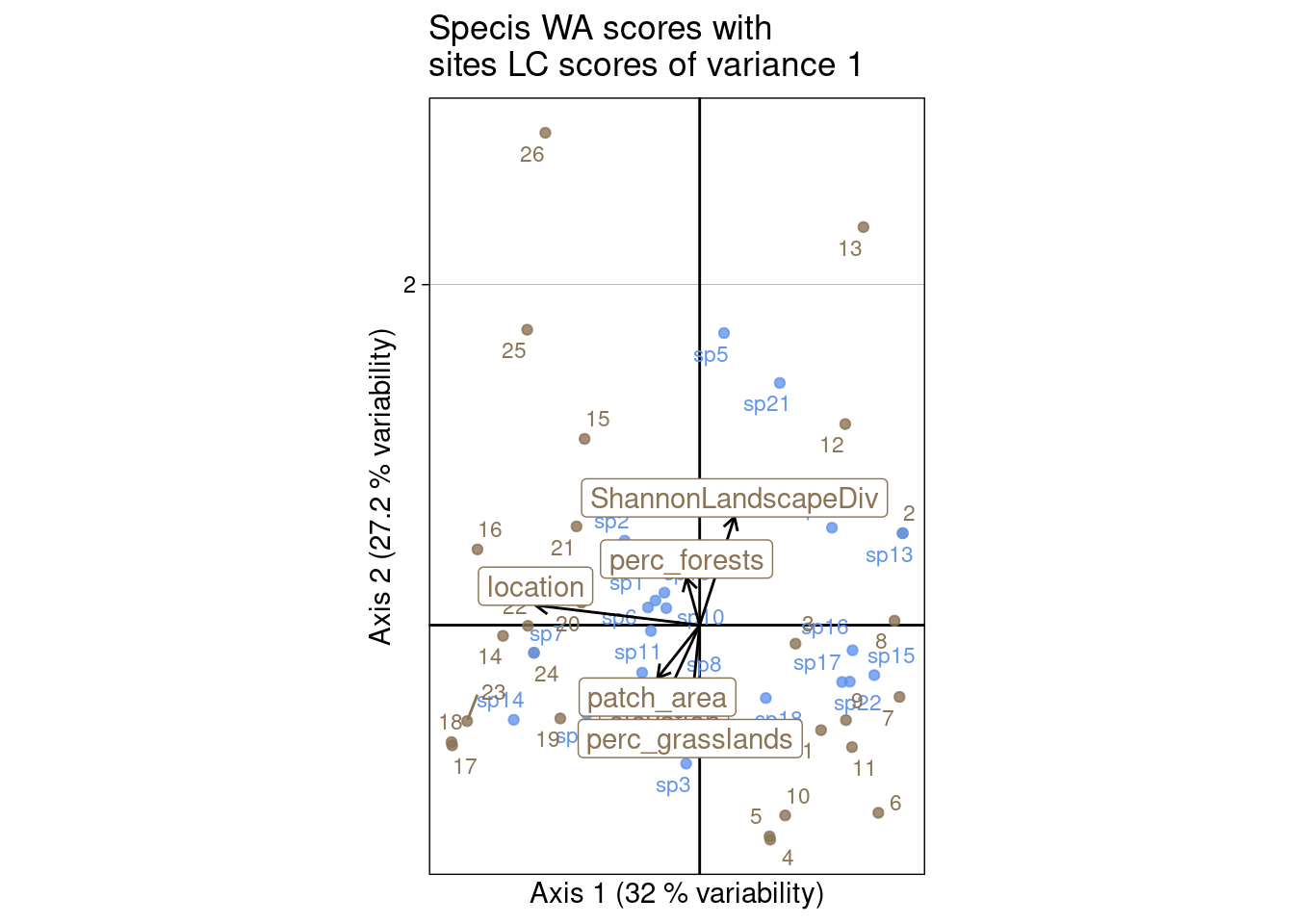

Code

s.label(cca$l1, # Predicted sites scores of variance 1
        plabels.optim = TRUE,
        plabels.col  = params$colsite,
        ppoints.col = params$colsite,
        main = "Specis WA scores with\nsites LC scores of variance 1")
s.label(cca$co, # Species WA
        plabels.optim = TRUE,
        plabels.col  = params$colspp,
        ppoints.col = params$colspp,
        add = TRUE)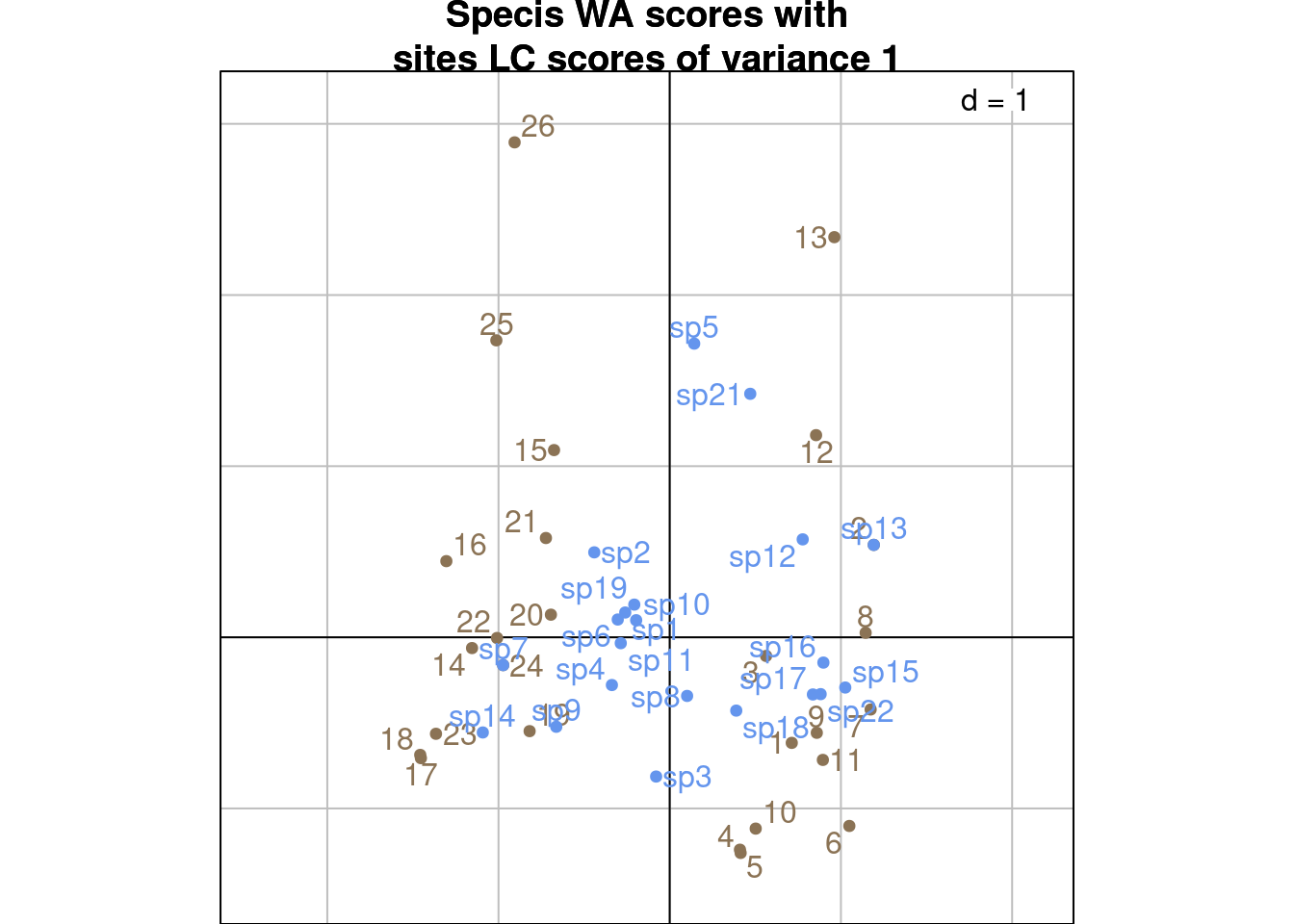

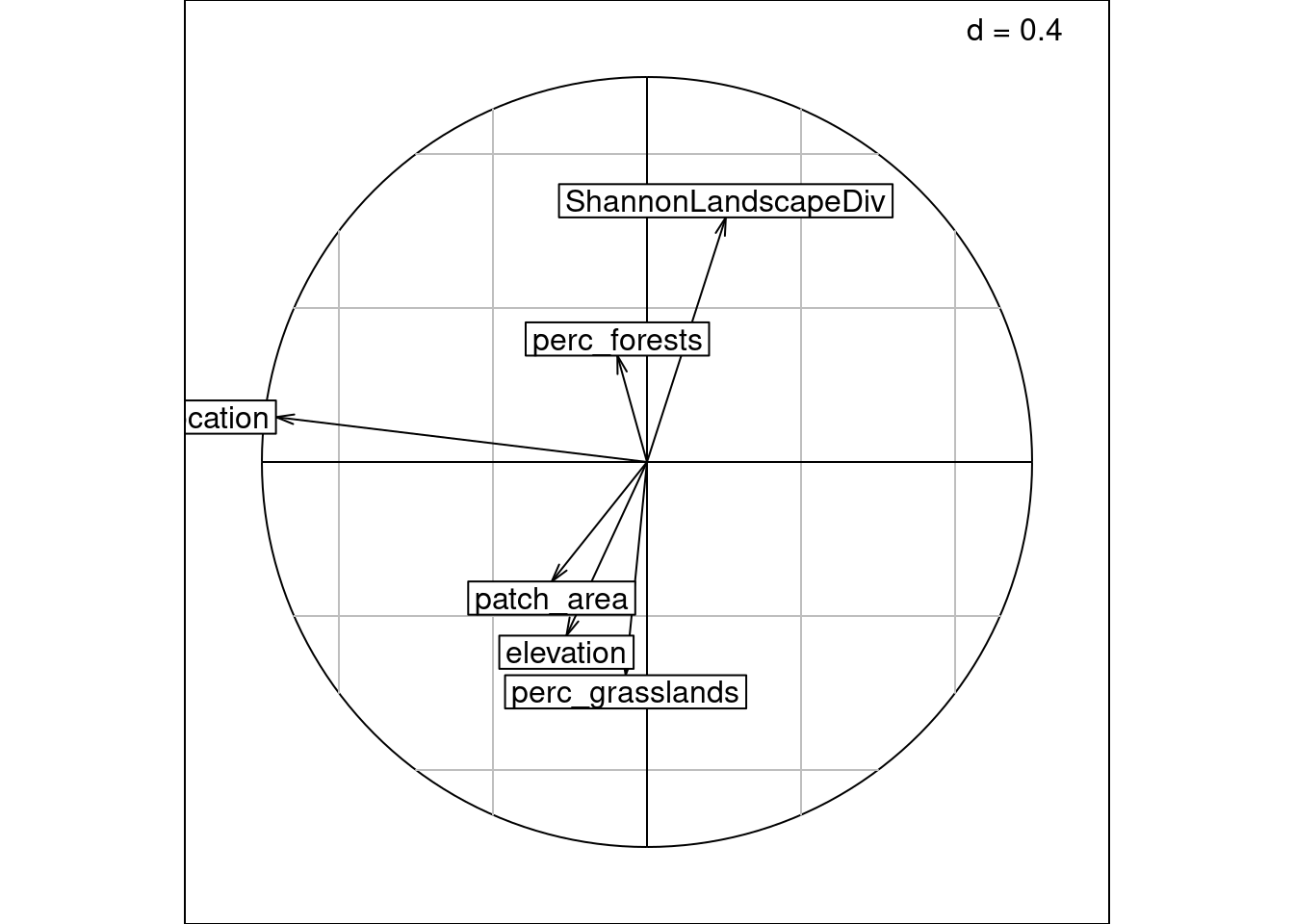
Code

s.corcircle(cca$cor)

We can also plot columns WA scores (\(V^\star\)/co) with the sites observed scores (\(U\)/“ls1” (not computed by ade4)):

Code

# WA scores
multiplot(indiv_row = U, indiv_col = Vstar, 
          indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y), 
          var_row = BS2, var_row_lab = colnames(E),
          row_color = params$colsite, col_color = params$colspp,
          mult = mult,
          eig = lambda) +
  ggtitle("Specis WA scores with\nsites observed scores of variance 1")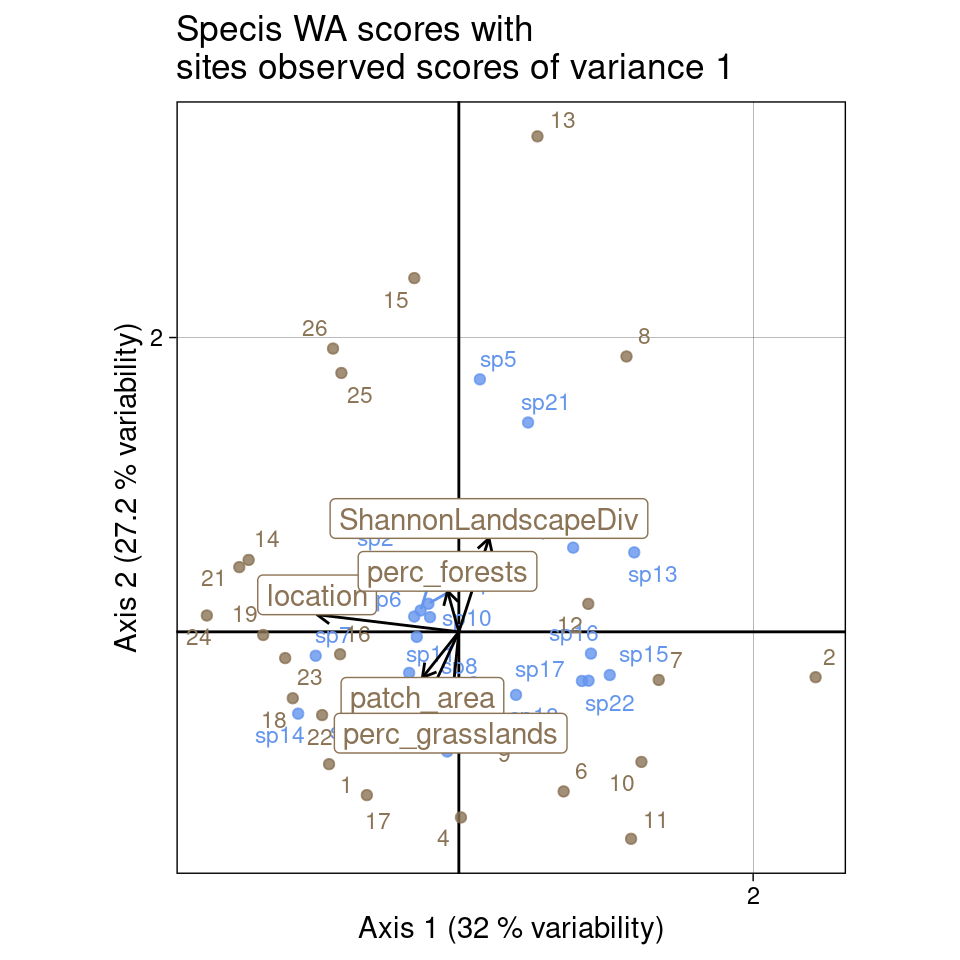

ade4 does not compute the sites observed scores normed at 1 (corresponding to \(U\)), so we compute them as \(\text{ls1} = \text{ls} \Lambda^{-1/2}\):

Code

as.matrix(cca$ls) %*% diag(lambda^(-1/2))

          [,1]        [,2]        [,3]        [,4]        [,5]         [,6]
1  -0.88194233 -0.89920813 -0.21510290 -0.75716763 -3.36433191  5.943824594
2   2.42444621 -0.30829774 -3.35321943  0.55963296  2.02916596  2.065563431
3  -0.34444473 -0.54181178 -0.08013664  0.57546029 -0.80398947  0.006814482
4   0.01419785 -1.26123684  1.34364884  1.79619359  1.59088842  1.764336111
5   0.04325107 -0.64051246  0.03049116  1.11682527 -0.74470162  1.355608210
6   0.71217106 -1.08445507  0.05021373  0.26782893  0.82751939 -1.185111342
7   1.35808644 -0.32688745  1.36849015 -0.06717237  1.40265285 -1.169991512
8   1.13927090  1.87131126  0.51489605  1.22937814 -1.90204431 -1.972136233
9   0.18631749 -0.69064739  1.56174573  0.49605602 -1.54800058 -1.044143121
10  1.24074453 -0.88393142  1.11709208 -1.88081630 -1.87523745  0.694839896
11  1.17040343 -1.40649896 -1.45445191  0.15749382 -0.70665751 -1.226713778
12  0.87979967  0.19023028  1.61346288 -0.66352718 -0.77675967 -1.410272996
13  0.53426380  3.36712361  1.01348658 -1.59561837  1.77100897  1.536210292
14 -1.42844996  0.48874250 -0.51552864  0.83759576 -1.39780352 -0.793502333
15 -0.30279177  2.40395635 -0.90288926 -0.17353516  3.64804877  0.066157822
16 -0.80715875 -0.15220790 -0.00359762  1.08059321  0.72058755  2.171252757
17 -0.62521546 -1.10958406  0.42720293  0.71161391 -0.28552526  2.455843219
18 -1.12871615 -0.45121491  0.52408704  1.79661165 -0.46072861  0.013919785
19 -1.32962334 -0.02131165  0.22268095 -1.76305566  2.21983155 -0.645198949
20 -0.71010429 -0.50179403  0.79488259  1.57807386  1.63438894 -2.298299831
21 -1.49191348  0.43981741 -0.22249008  1.27068234 -1.31901558 -0.764324772
22 -0.92914770 -0.56566757  0.17354832  0.51597625  0.01408031 -0.288080450
23 -1.18010511 -0.17836577 -0.02322108 -2.68084807  3.05668242  0.997011359
24 -1.71254285  0.11121758 -1.76025623 -2.07277698 -1.45573752 -2.393217624
25 -0.79823857  1.75933428 -0.09999050  0.83358035 -3.48847449 -0.953485788
26 -0.85502843  1.92516632  0.29281684  1.85795073 -2.41935625 -0.211052481

Code

s.label(ls1_ade4, # Sites WA scores U
        plabels.optim = TRUE,
        plabels.col  = params$colsite,
        ppoints.col = params$colsite,
        main = "Specis WA scores with\nsites observed scores of variance 1")
s.label(cca$co, # Species WA
        plabels.optim = TRUE,
        plabels.col  = params$colspp,
        ppoints.col = params$colspp,
        add = TRUE)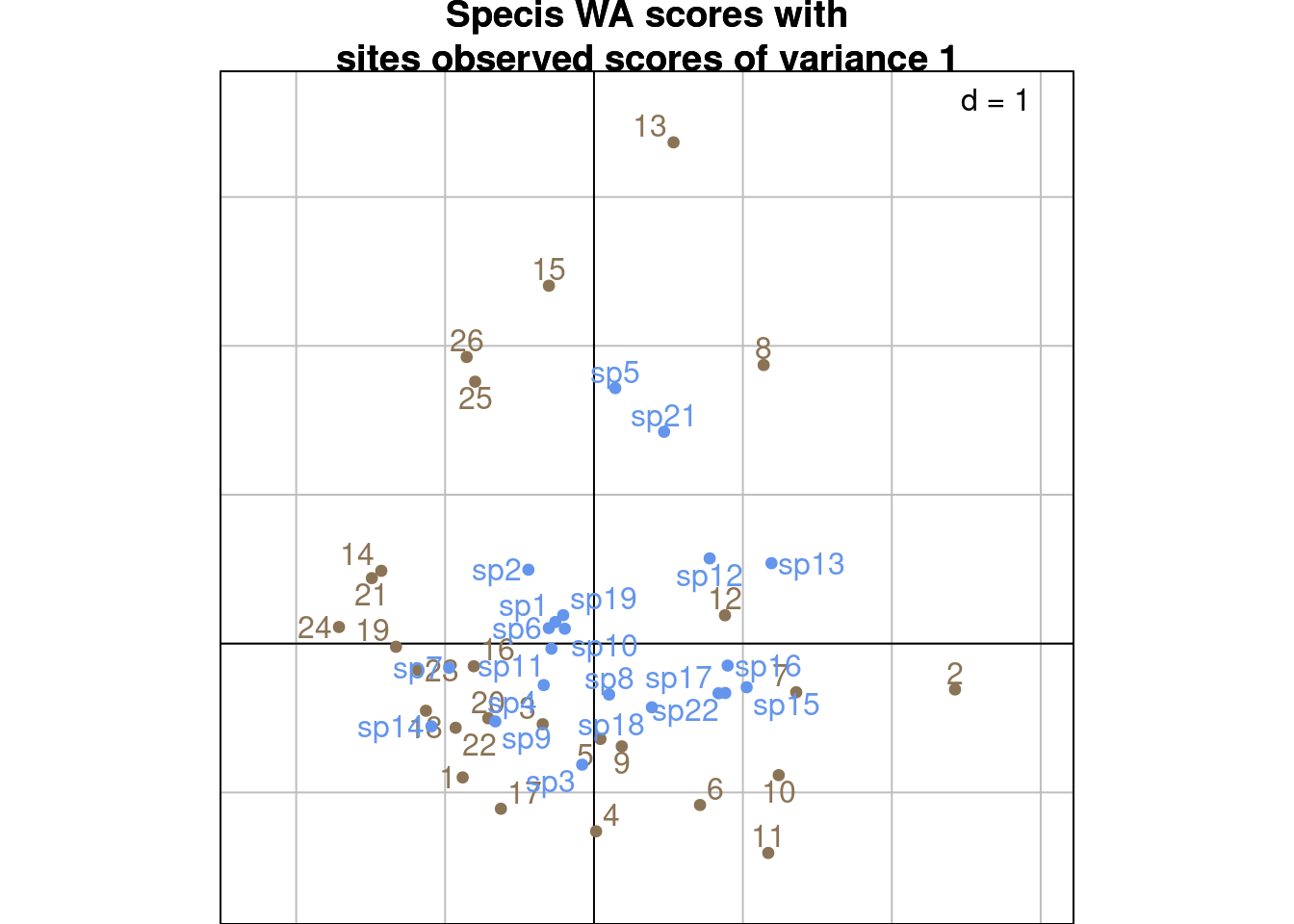

Scaling type 3

This type of scaling is a compromise between scalings type 1 and 2.

the rows (sites) scores can be \(\hat{S}_3 = U \Lambda^{1/4}\) or \(Z_3 = D_r^{-1/2} \hat{P_0} V_0 \Lambda^{-1/4}\)
the columns (species) scores are \(S_3 = V \Lambda^{1/4}\)
the explanatory variable score are \(BS_3 = E_{stand}^\top D_r Z_{stand} \Lambda^{1/4}\)

# Row scores
Shat3 <- U %*% Lambda^(1/4) # Latent scores
Z3 <- diag(dr^(-1/2)) %*% P0hat %*% V0 %*% diag(lambda^(-1/4)) # Predicted scores

# Columns scores
S3 <- V %*% Lambda^(1/4)

# Variables correlation
BS3 <- t(Estand) %*% Dr %*% Zstand %*% Lambda^(1/4)

The corresponding ade4 values are not computed, but we can compute them:

Z3_ade4 <- as.matrix(cca$l1) %*% diag(cca$eig^(1/4))
Shat3_ade4 <- ls1_ade4 %*% diag(cca$eig^(1/4))
S3_ade4 <- as.matrix(cca$c1) %*% diag(cca$eig^(1/4))

all(abs(abs(Z3_ade4/Z3) - 1) < zero) # LC scores for sites

[1] TRUE

all(abs(abs(Shat3_ade4/Shat3) - 1) < zero) # sites scores

[1] TRUE

all(abs(abs(S3_ade4/S3) - 1) < zero) # species scores

[1] TRUE

Plots

Code

# LC scores
multiplot(indiv_row = Z3, indiv_col = S3, 
          indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y), 
          var_row = BS3, var_row_lab = colnames(E),
          row_color = params$colsite, col_color = params$colspp,
          mult = mult,
          eig = lambda) +
  ggtitle("LC scores for sites")

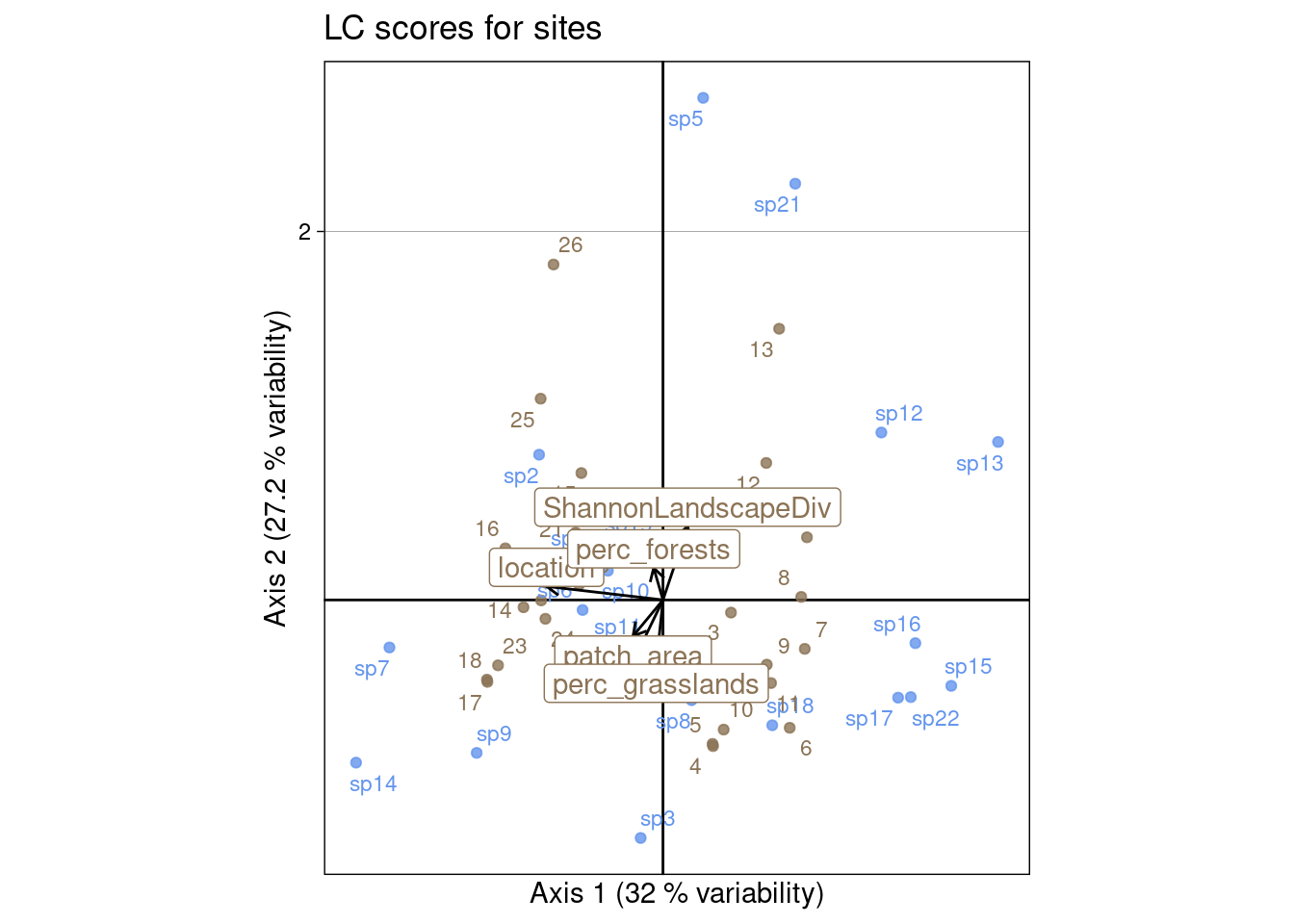
s.label(Z3_ade4,
        plabels.optim = TRUE,
        xlim = c(-3, 2),
        ylim = c(-2, 3),
        plabels.col  = params$colsite,
        ppoints.col = params$colsite)
s.label(S3_ade4,
        plabels.optim = TRUE,
        plabels.col  = params$colspp,
        ppoints.col = params$colspp,
        add = TRUE)

Code

mult <- 5

multiplot(indiv_row = Shat3, indiv_col = S3, 
          indiv_row_lab = rownames(Y), indiv_col_lab = colnames(Y), 
          var_row = BS3, var_row_lab = colnames(E),
          row_color = params$colsite, col_color = params$colspp,
          mult = mult,
          eig = lambda) +
  ggtitle("Sites latent scores")

s.label(Shat3_ade4,
        plabels.optim = TRUE,
        xlim = c(-3, 2),
        ylim = c(-2, 3),
        plabels.col  = params$colsite,
        ppoints.col = params$colsite)
s.label(S3_ade4,
        plabels.optim = TRUE,
        plabels.col  = params$colspp,
        ppoints.col = params$colspp,
        add = TRUE)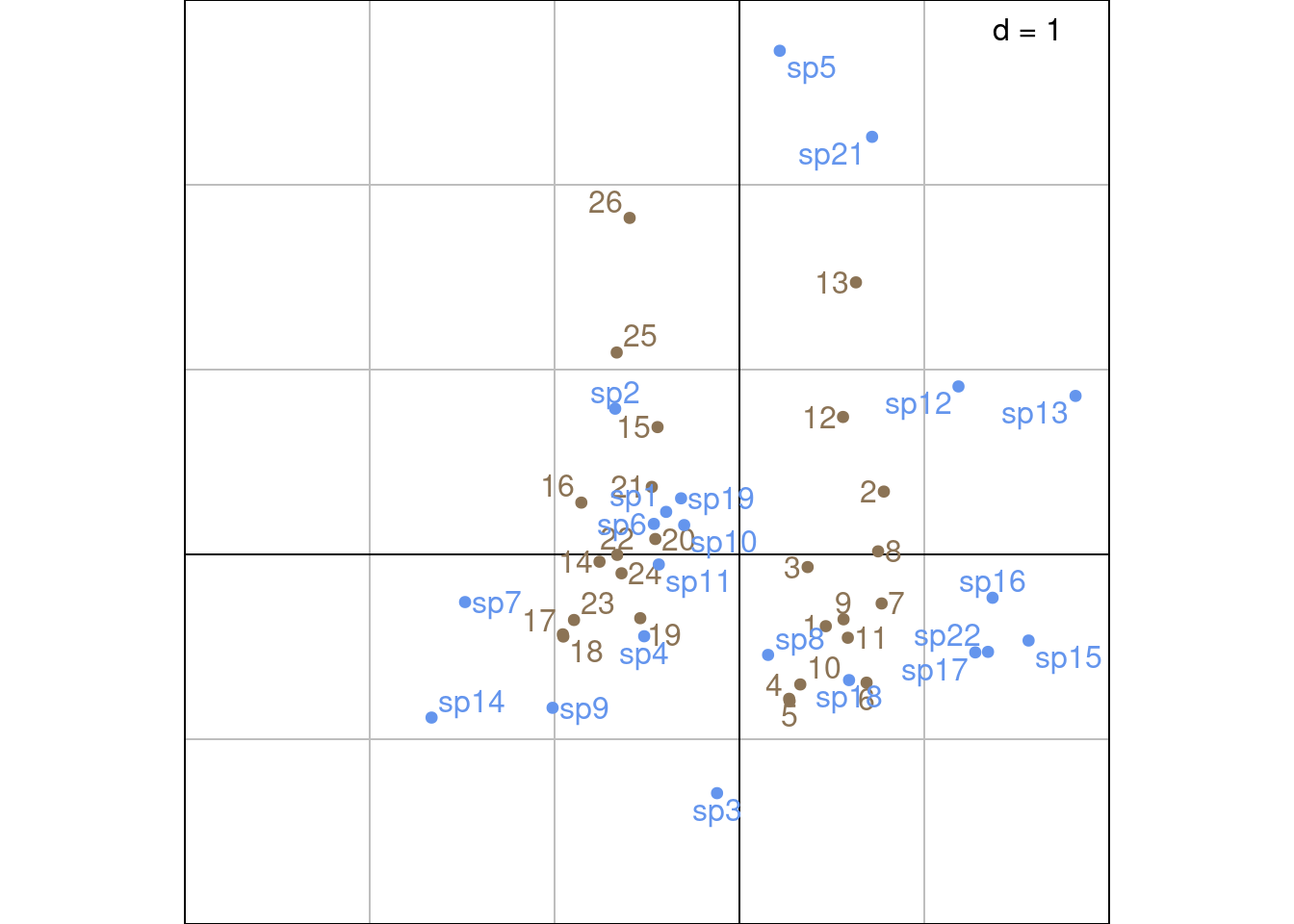

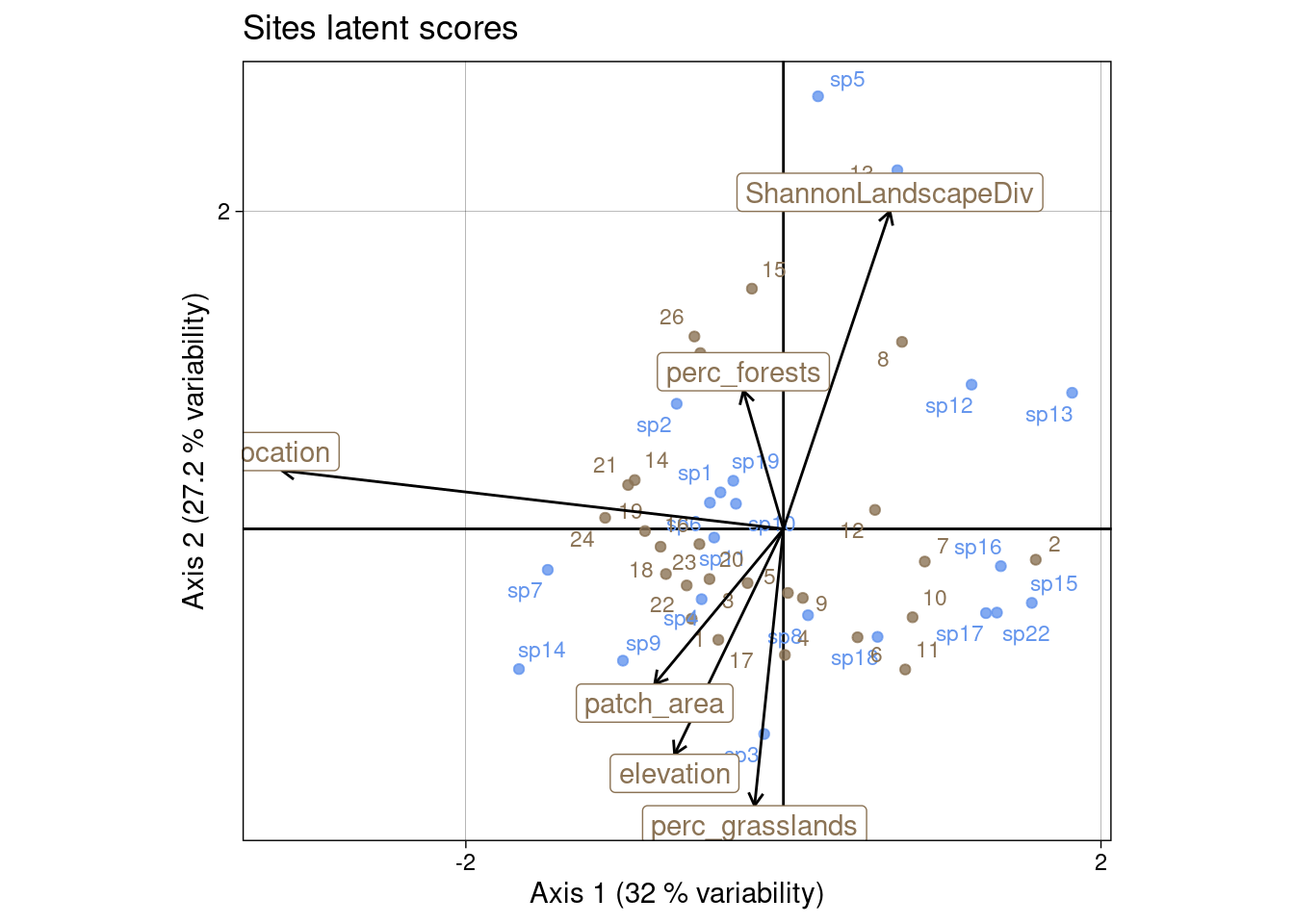
Interpretation

In CCA, each ordination axis corresponds to a linear combination of the explanatory variables that maximizes the explained variance in the response data.

This analysis constrains rows (sites) scores to be linear combinations of the environmental variables (scaling \(Z_i\)).

Species can be ordered along environmental variables axes by projecting species coordinates on the vector of this variable. This gives species niche optimum, but there are strong assumptions:

unimodal distribution of niches preferences along the variable of interest
species distributions are indeed controlled by the environment
the study gradient is long enough to capture the range of species abundance variation.

The part of variation explained by the environmental variables can be computed as

\[ \frac{\sum_k \lambda_k(CCA)}{\sum_l \lambda_l(CA)} \]

sum(lambda)/sum(ca$eig)

[1] 0.3795835

Here, the environmental variables explain 38 % of the total variation.

Warning: in CCA, using noisy or not relevant explanatory variables leads to spurious relationships.

Residual analysis

In order to examinate residuals, a CA can be performed on the table of residuals \(P_{\text{res}}\):

\[ P_{\text{res}} = P_0 - \hat{P}_0 \]

Pres <- P0 - P0hat

res_pca <- dudi.pca(Pres, scannf = FALSE, nf = 27)

scatter(res_pca)

Tests of significance

It is possible to test the significance of the the relationship between \(E\) and \(Y\) with a permutation test.

randtest(cca, nrepet = 999)

Monte-Carlo test
Call: randtest.pcaiv(xtest = cca, nrepet = 999)

Observation: 0.3795835 

Based on 999 replicates
Simulated p-value: 0.001 
Alternative hypothesis: greater 

     Std.Obs  Expectation     Variance 
3.6166911230 0.2672678214 0.0009644016

References

Legendre, P., and Louis Legendre. 2012. Numerical Ecology. Elsevier.